Aprendizaje basado en problemas y estructura multiplicativa: diseño y aplicación de un modelo de formación matemática para el rendimiento académico en básica primaria

Problem-based learning and multiplicative structure: design and application of a mathematical training model for academic performance in primary school

Bernardo José González Ascencio¹ y Francisco Javier Gómez²

¹Universidad UMECIT de Panamá, bernardojosegonzalezascencio@gmail.com, https://orcid.org/0009-0007-0340-2899, Colombia

²Universidad UMECIT de Panamá, franciscogomez.doc@umecit.edu.pa, https://orcid.org/0009-0008-0135-1212, Colombia

	Información del Artículo	RESUMEN
	Trazabilidad: Recibido 11-08-2025 Revisado 12-08-2025 Aceptado 17-09-2025	El presente articulo científico con el objetivo de evaluar el impacto del Aprendizaje Basado en Problemas (ABP) y pedagogía didáctica de la estructura multiplicativa en el rendimiento académico del área de matemáticas, en estudiantes de grado quinto de primaria, en la ciudad de Barranquilla, Colombia. Este estudio, con un enfoque cuantitativo y diseño cuasiexperimental, con la aplicación de Pretest y postes en grupos no equivalentes, además de pruebas estandarizadas, cuestionarios estructurados y análisis comparativo de resultados en estudiantes y docentes de matemáticas. A partir, de un diagnóstico inicial se pudo evidenciar vacíos en los conceptos de interpretación de problemas multiplicativos, por lo que se implanta un modelo pedagógico basado en situaciones contextualizadas, usando el trabajo colaborativo y análisis de relaciones numéricas. Ahora bien, los resultados muestran avances bastante importantes en los grupos, en la resolución de problemas y la argumentación de procedimientos matemáticos usados, tanto en estudiantes como en docentes. Esta investigación resalta la importancia de la inclusión dentro del proceso de enseñanza y aprendizaje el uso de las tecnologías de la información y comunicación como un factor determinante que ayuda en la motivación de los alumnos a comprender los concentos matemáticos. Finalmente, se concluye que el ABP, en sintonía con la enseñanza de la multiplicación, puede favorecer el desarrollo del pensamiento matemático, haciéndolo más analítico, flexible y situado, viéndola como una estrategia eficaz para el mejoramiento del aprendizaje en contextos escolares.
	Palabras Clave: Aprendizaje basado en problemas Enseñanza de las matemáticas Resolución de problemas Trabajo colaborativo Estructura multiplicativa Educación primaria
Keywords: Problem based on learning Teaching mathematics Problem solving Collaborative work Multiplicative structure Primary education		ABSTRACT This scientific article aims to evaluate the impact of Problem-Based Learning (PBL) and the multiplicative structure teaching method on academic performance in mathematics among fifth-grade students in the city of Barranquilla, Colombia. This study, with a quantitative approach and quasi-experimental design, involved the application of pre- and post-tests in non-equivalent groups, as well as standardized tests, structured questionnaires, and comparative analysis of results in students and mathematics teachers. Based on an initial diagnosis, gaps in the concepts of interpreting multiplicative problems were identified, leading to the implementation of a pedagogical model based on contextualized situations, using collaborative work and analysis of numerical relationships. The results show significant progress in the groups in problem solving and the reasoning behind the mathematical procedures used, both in students and teachers. This research highlights the importance of including the use of information and communication technologies in the teaching and learning process as a determining factor that helps motivate students to understand mathematical concepts. Finally, it concludes that PBL, in line with the teaching of multiplication, can promote the development of mathematical thinking, making it more analytical, flexible, and situated, and seeing it as an effective strategy for improving learning in school contexts.

INTRODUCCIÓN

El siguiente informe reconoce y estudia la enseñanza de las matemáticas en la Educación básica primara para el desarrollo cognitivo y practico de los estudiantes. Esto, es fundamental para una formación integral, contribuye, además con un constante desarrollo del pensamiento, capacidad crítica de análisis y resolución de problema en los distintos contextos en los que se desenvuelve cada estudiante. Sin embargo, aunque se muestra que es de mucha importancia el enfoque del estudio hacia esta área, representa un reto ya que, en el contexto de un país como Colombia, existen ciertos desbalances y limitaciones, enmarcadas por la desigualdad socioeconómica, las dificultades para el acceso a herramientas y recursos que facilitan el aprendizaje. específicamente, en la ciudad de Barranquilla, esto puede verse reflejado en el bajo desempeño académico, particularmente en los grados tercero y quinto de primaria, lo cual pone en evidencia la necesidad de hacer un ajuste en las estrategias pedagógicas que se utilizan en la enseñanza de las matemáticas.

Ahora bien, como respuesta a dicha problemática, en el presente estudio se plantea la implementación de metodologías activas y participativas, que estén focalizadas en el aprendizaje basado en proyectos (ABP) y la enseñanza de la estructura multiplicativo, como una estrategia que sea de ayuda para mejorar el rendimiento en el área de matemáticas. Como menciona Hmelo “la adopción efectiva del ABP dependen en gran medida del contexto educativo, en especial de la cultura escolar y la disponibilidad de recursos para la profesionalización docente” (2004, p.22). Por tanto, estas técnicas al estar centradas en el alumno y en la manera en la que estos son capaces de resolver problemas de la cotidianidad, pueden ayudar a contextualizar el aprendizaje y así llevarlos a una motivación y facilitar el aprendizaje de los contenidos del área. Por lo tanto, este estudio propone como objetivo principal evaluar el impacto de estas estrategias en el desarrollo del aprendizaje de los estudiantes de gado quinto en instituciones educativas de la ciudad de barranquilla, teniendo en cuenta sus contextos sociales, culturales y los limitantes a los que se enfrentan.

Este estudio, con un enfoque cuasiexperimental, con aplicación de propuestas Pretest y Postest en diferentes grupos, implementa una intervención pedagógica que tiene como fin diagnosticar, intervenir y analizar las mejoras en los niveles del desempeño académico y la comprensión de las temáticas propuestas en el área de matemáticas. Es desarrollado en instituciones educativas oficiales de la ciudad de barranquilla, y busca evaluar el impacto del modelo de formación matemática basado en el ABP y en la estructura multiplicativa sobre el rendimiento académico de los estudiantes de grado quinto. Además, esta investigación no solo tiene como propósito constatar el impacto que tiene este modelo innovador y didáctico en la enseñanza de las matemáticas, sino también hacer aportes a la transformación de esta en contextos vulnerables. Partiendo del hecho de que una educación de calidad no puede desvincularse de factores como lo social y lo cultural, por lo que se proponen estas estrategias que logren responder las necesidades de los estudiantes en sus diferentes contextos, para fortalecer su rendimiento académico, su motivación y su participación.

Finalmente, el objetivo general de esta investigación es evaluar el impacto de un modelo de formación para la enseñanza de las matemáticas, que se fundamenta en el Aprendizaje Basado en problemas y en el tratamiento didáctico de la estructura multiplicativa, en lo que respecta al rendimiento académico de los estudiantes del grado quinto. Específicamente, esta investigación propone poder diagnosticar los niveles de desempeño en la resolución de problemas multiplicativos, además de diseñar una propuesta didáctica que vaya de acuerdo con el contexto, aplicar dicha propuesta en contextos reales donde haya vulnerabilidad educativa y así, analizar las disparidades en el desempeño entre los estudiantes que hicieron parte del proyecto y aquellos que no. Este enfoque tiene como fin aportar elementos importantes para mejorar la enseñanza de las matemáticas en la educación primaria, además de promover la equidad, la innovación pedagógica y el desarrollo de competencias en distintos contextos escolares. De lo anterior surge la pregunta: ¿Cuál es el impacto que tiene la aplicación de un modelo de formación orientado por el aprendizaje basado en problemas y la estructura multiplicativa sobre el rendimiento matemático en estudiantes de grado quinto nivel básica primaria?.

MATERIALES Y MÉTODOS

El presente estudio se fundamenta a partir de un paradigma positivista que responder a la necesidad de establecer relaciones objetivas entre variables que puede ser observadas y medidas se asume una posición epistemológica que ve la realidad como algo que está por fuera del individuo que investiga, por lo que busca analizar y explicar fenómenos a partir de datos cuantitativos de manera rigurosa (Hernández et al., 2018). Además que cuenta con un enfoque cuantitativo, con un diseño cuasiexperimental de tipo Pretest y Postest, con un grupo control y grupo experimental. Dicho enfoque permite la posibilidad de evaluar el impacto de un modelo de formación matemática centrado en el Aprendizaje Basado en Problemas (ABP) y en la enseñanza de la estructura multiplicativa, a fin de realizar ciertas comparaciones entre los resultados obtenido al principio y al final de la intervención pedagógica (Hurtado, 2010). Gracias a esto se pueden obtener datos concisos y objetivos que pueden servir como base para un futuro análisis de investigaciones dentro del contexto educativo.

El diseño de investigación tiene un enfoque transeccional contemporáneo multivariable de diferentes fuentes que se alinea con dicho paradigma positivista y además con el enfoque cuantitativo. Este diseño, es capaz de responder a acciones necesarias dentro del enfoque como describir, comparar y analizar diferentes variables que están relacionadas entre sí. Esta estrategia permite comparar datos cuantitativos de diferentes fuentes con un mismo procedimiento estadístico. Lo cual hace posible que los resultados de la investigación puedan ser más confiables, sin utilizar herramientas cuantitativas, dentro del proceso de análisis (García, 2020). Con la aplicación de una propuesta didáctica basada en ABP, que está estructurada en pro de la resolución de conflictos contextualizados, que involucren el concepto de multiplicación una relación entre conjuntos, se logra analizar el impacto de esta estrategia. La siguiente tabla contiene las diferentes variables de investigación, dimensiones e ítems

Tabla 1: Variables de investigación

Variable	Dimensión	Ítems
ABP aprendizaje basado en problemas	Contenido	Selecciono cuidadosamente el contenido disciplinar que debe abordarse en el problema, garantizando la correspondencia con los referentes de calidad. Los problemas que planteo en el aula promueven el desarrollo de habilidades cognitivas profundas relacionadas con el contenido específico. Diseño problemas contextualizados que se relacionan con situaciones reales y cercanas al contexto de los estudiantes. Los problemas que presento permiten establecer conexiones entre distintos conceptos, áreas del saber o situaciones cotidianas. Fomento que los estudiantes integren conocimientos previos con nuevos aprendizajes al resolver problemas.
	Contexto
	Conexión
Estructura multiplicativa	Proporcionalidad directa simple/Razón/Isomorfismo de medidas	En la sesión de clase de matemáticas explico el concepto de razón y su relación con la multiplicación y la división. Fomento en el salón de clases el manejo de tablas de proporcionalidad para resolver problemas con razón constante.
	Producto de medidas/Producto cartesiano/Combinación	Reconozco cuando un problema aritmético se relaciona con producto de medidas o una combinación de elementos. Utilizo problemas de producto cartesiano para que los estudiantes desarrollen el pensamiento numérico.
	Comparación/Factor multiplicante	Comprendo el rol del factor multiplicante en los problemas matemáticos que propongo a los estudiantes. Modelas situaciones que integren el factor multiplicante en los problemas desarrollados en clase.
	Proporcionalidad compuesta/Conversión	Identifico con claridad los problemas que requieren el uso de múltiples razones para solucionarlos. Integro situaciones que implican conversiones entre unidades en los momentos de estructuración para enseñar proporcionalidad.
Enseñanza de la resolución problemas en matemáticas	Tipos de problemas	Identifico con claridad las diferencias entre problemas aritméticos de estructura multiplicativa simple y compuestos, y propongo ejemplos de cada caso. Reconozco las distintas formas en que pueden disponerse las proposiciones en un problema aritmético verbal de estructura multiplicativa. Puedo diseñar problemas aritméticos de enunciado verbal de estructura multiplicativa cambiando el orden de las proposiciones.
	Estrategias para resolver problemas de Razón	Utilizo problemas contextualizados que permiten a los estudiantes aplicar estrategias como la realista, de reparto o agrupamiento. Promuevo en el aula el uso de esquemas, diagramas o dibujos para representar problemas de razón. Guío a los estudiantes para que exploren soluciones aditivas con agrupaciones, duplicaciones, de reparto, de ensayo y error, con resta reiterada antes de introducir algoritmos de multiplicación o división. Fomento el uso de estrategias multiplicativas como la descomposición, el algoritmo, mitades, de ensayo y error, división.
Estrategias pedagógicas	Planeación	Durante la etapa de planeación enfoco la metodología de la clase en el ABP.
	Enseñanza	Durante la etapa de estructuración y transferencia desarrollo elementos del ABP.
	Evaluación formativa	Aplico rúbricas para valorar las competencias en resolución de problemas. Realizo retroalimentación continua sobre el proceso. Promuevo la autoevaluación y coevaluación entre los estudiantes. Uso la evaluación como medio para mejorar la enseñanza.

La población de esta investigación está conformada por estudiantes de grado quinto de instituciones educativas de la ciudad de barranquilla. Este estudio se centra en diez instituciones educativas oficiales del distrito de branquilla por su ubicación geográfica adecuada para trabajar con el respectivo grado, se tienen en cuenta una población total de 826 estudiantes y 33 docentes de estas diez instituciones. La muestra se dio a partir de un muestreo no probabilístico intencional, el cual estuvo compuesto por dos grupos, uno experimental y otro de control. El total de instituciones participantes son dos, contando con el cuerpo docente como parte del estudio, 205 estudiantes y 11 docentes, de la institución Educativa Ciudadela 20 de Julio e Institución Educativa Miguel Ángel Buile. Como se observa en la siguiente tabla:

Tabla 2: Descripción de la muestra

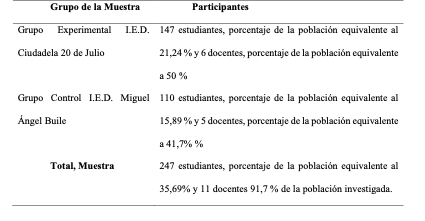
La recolección de los datos se da por medio de tres instrumentos principales, en primer lugar, una prueba diagnóstica que se centra en la resolución de problemas de estructura multiplicativa, en segundo lugar, una encuesta a estudiantes para observar sus actitudes frente a las matemáticas, en tercer lugar, un cuestionario dirigido a los docentes a cerca de sus prácticas pedagógicas. La triangulación de estos instrumentos ha hecho posible identificar algunos factores cualitativos que están vinculados a la motivación, la participación y la apropiación de conceptos, además de medir el rendimiento académico de los estudiantes. Y la metodología consta de tres fases, la diagnostico inicial, diseño e implementación de la propuesta didáctica y la evaluación del impacto de esta.

El análisis de datos se realiza a partir del software SPSS, en donde se aplican técnicas de estadística descriptica e inferencial, además se aplican pruebas de normalidad (Kolmogorov Smirnov y Shapiro Wilk), y la prueba t de Student para muestras independientes y la prueba U de Mann Whitney, teniendo en cuenta la distribución de datos. Estas herramientas hacen que al contrastar los resultados entre ambos grupos; el de control y experimental se pueda evaluar el efecto de la intervención sobre el rendimiento académico en el área de matemáticas. En suma, el rigor de esta investigación no esta delimitada por la valides estadística de sus instrumentos, sino que también se fundamenta en una implementación que lleve a la reflexión, desde el punto de vista de un dialogo constante entre el contexto educativo, la comunidad educativa en general y la teoría que busca la innovación didáctica dentro de las aulas de clase. 

RESULTADOS

Los resultados que se obtuvieron luego de la implementación del modelo didáctico fundamentado en el Aprendizaje Basado en Problemas (ABP) y la estructura multiplicativa, deja ver cambios significativos en el proceso de enseñanza y aprendizaje de las matemáticas en los estudiantes de grado quinto. Partiendo del análisis comparativo entre los grupos experimental y el grupo de control, donde se pudo identificar mejoras destacables en el rendimiento académico, la comprensión del concepto de multiplicación, además de un cambio positivo en la actitud de los estudiantes hacia las matemáticas y una respuesta receptiva a la participación en las actividades escolares. Esto demuestra lo mencionado por Strobel y Barnevel (2009) cuando mencionan que estas metodologías “incrementan la motivación intrínseca del estudiante y mejoran la aplicación de los conocimientos”. Dichos cambios o transformaciones fueron muy evidentes en el grupo experimental, el cual hizo parte de la propuesta pedagógica aplicada y diseñada en esta investigación.

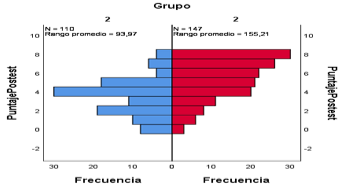
Fi. 1: Grafico de barras dobles Postest de los estudiantes del grupo de control y experimental.

Estos cambios y transformación son solo indican cifras cuantificables, sino que también se ve reflejado en las interacciones en el aula, el cambio actitudinal de los estudiantes, su disposición a enfrentar problemas matemáticos y la apropiación y uso del lenguaje matemático. Dichas mejoras evidencian que el modelo se utilizo tuvo un gran impacto en el proceso formativo, de una forma integral ya que fue capaz de abordar el desarrollo cognitivo y los factores actitudinales y emocionales que se asocian con el aprendizaje. Asimismo, los docentes también expresaron cambios en sus prácticas pedagógicas y una mayor conciencia para darle la importancia debida al contextualizar los contenidos matemáticos para una mejor comprensión de estos, lo que demuestra que este enfoque es efectivo en su aplicación.

Los cambios no se limitaron a indicadores cuantitativos, sino que se reflejaron también en las interacciones en el aula, la disposición de los estudiantes a enfrentar desafíos matemáticos y la apropiación del lenguaje matemático. Estas mejoras sugieren que el modelo utilizado tuvo un impacto integral en el proceso formativo, abordando tanto el desarrollo cognitivo como los factores actitudinales y emocionales asociados al aprendizaje. Asimismo, los docentes manifestaron cambios en sus prácticas pedagógicas y una mayor conciencia de la importancia de contextualizar los contenidos matemáticos, lo que refuerza la pertinencia del enfoque adoptado. Sabiendo que cualquier cambio que se dé después en el desempeño puede ser adjudicado a la intervención (Hernández et al., 2014).

Análisis de resultados

Comprensión conceptual de la multiplicación

Esta dimensión clave, la comprensión conceptual de la estructura multiplicativa dejó ver que, tras la intervención, los estudiantes del grupo experimental pudieron distinguir como mucha más claridad los distintos significados y aplicación de la multiplicación en contextos reales, viendo más allá de la visión cuadrada y mecánica de las matemáticas. Este cambio fue notorio en la forma en la que resolvían problemas de reparto, comparación y proporcionalidad, usando estrategias que se adaptarla contexto. Tal como lo plantea Vergnaud (1996), que señala que el desarrollo del pensamiento multiplicativo no solamente se limita a la memorización de tablas o la realización de algoritmos, sino que más bien es necesaria la construcción de estructuras cognitivas que puedan hacer que el estudiante tenga la habilidad de interpretar de manera significativa los datos numéricos. Por tanto, esta propuesta logro que dichas estructuras se activaran, mediante la aplicación de problemas reales, diálogos matemáticos y representaciones múltiples permitiendo que los estudiantes construyan ideas y nociones solidas sobre los conceptos básicos de matemáticas.

Resolución de problemas contextualizados          

En cuanto a la resolución de problemas contextualizados, se mostró un gran progreso en la capacidad de los estudiantes para lograr enfrentar ciertas situaciones, poder identificar los datos relevantes, seleccionar los procedimientos adecuados y llegar a poder argumentar sus respuestas. En un contraste con el grupo de control y el grupo experimental, el primero mostró ciertas dificultades para la interpretación de situaciones problemáticas y se apoyaba más en secuencias lógicas, el segundo grupo pudo realizar y aplicar estrategias variadas y flexibles, lo cual demuestra una comprensión más profunda de los problemas planteados. Lo cual se alinea con lo propuesto por Polya (1957), en la resolución de problemas donde se debe entender, crear un plan, ejecutarlo y revisar la solución para verificar su eficacia. Teniendo en cuenta esto, que trabajar estos problemas contextualizados, hizo posible que los estudiantes pudieran relacionar los contenidos escolares con sus propias experiencias, para llevarlos a un aprendizaje significativo que fortalezca su motivación.

Participación activa y trabajo colaborativo

La implementación de este modelo didáctico también hizo posible el fomento de una mayor participación de los estudiantes dentro del aula de clases, en las que se dieron espacios para el trabajo colaborativo que llevaron a que los estudiantes intercambiaran ideas, construyeran soluciones conjuntas y pudieran reflexionar de manera critica. Estos espacios, permitieron que los estudiantes aprendieran a escuchar a sus compañeros, a argumentar y dar sus puntos de vista, a aceptar los errores como una parte importante del proceso de aprendizaje. Esto fue relevante para la mejora del desempeño en especial para los estudiantes que en un principio mostraban una baja participación en clases. Gracias a que el ABP genera ambientes de trabajo colaborativo, se pudo generar en los estudiantes curiosidad y motivación para aprender en clases (Calle et al., 2020).

Análisis estadístico

Los resultados estadísticos que se obtuvieron a partir del análisis de los datos demuestran la efectividad del modelo didáctico que se aplicó. Se utilizaron pruebas de normalidad; la t de Student para muestras independientes y la prueba U de Mann Whitney, lo cual hizo posible la comparación de ambos grupos en un antes y después de la aplicación de la estrategia. En la mayoría de los casos, hubo diferencias estadísticamente significativas a favor del grupo experimental respaldando la idea de esta investigación. Los porcentajes revelaron que el grupo experimental paso de tener un 60% de estudiante con niveles bajo y básico a un 70,7% con estudiantes en niveles altos y superior, mientas que el grupo control mantuvo una proporción similar entre el Pretest y el Postest. Lo que evidencia que la propuesta no solo genero aprendizajes significativos, sino que permitió que los estudiantes mejoraran su rendimiento académico. Esto demuestra la importancia del diseño cuasiexperimental como estrategia para evaluar intervenciones educativas en ambientes y contextos reales lo que aporta una evidencia clara para la toma de decisiones pedagógicas, siempre que se gestione de manera adecuada la intervención y se utilicen técnicas de estadísticas adecuadas (Hernández y Mendoza, 2018).

DISCUSIÓN

En términos generales, los resultados de esta investigación confirman que el modelo didáctico centrado en el ABP y la estructura multiplicativa es una herramienta muy efectiva que ayuda a mejorar el aprendizaje de las matemáticas en la educación primaria. Esta propuesta logró que los contenidos curriculares se adapten a las realidades del contextos y también a que los estudiantes desarrollen un pensamiento complejo y crítico, promoviendo una cultura en el aula más reflexiva y participativa, como lo menciona Barrows (1986), que dice que el ABP fomenta el aprendizaje activo y contextualizado lo que permite que los estudiantes usen todos sus conocimientos previos y los nuevos, llevándolos a relacionarlos con las experiencias propias y cotidianas, para que esto les ayude en la resolución de problemas y el aprendizaje significativo. De igual manera, la incorporación de la estructura multiplicativa como una base de la investigación, hizo posible el abordaje de contenidos temáticos más complejos desde una perspectiva contextualizada y por ende más significativa. Así como lo plantea Vergnaud (1996), al mencionar que el pensamiento multiplicativo requiere una creación de estructuras conceptuales que no están limitadas a la memorización de esquemas lógicos, sino que es importante que haya una interpretación y aplicación de dichas estructuras a la realidad de los contextos. Esto se observó en los participantes de este estudio, en específico en la resolución de problemas.

Ahora bien, desde una perspectiva pedagógica, este estudia demuestra que las metodologías activas que se centran en los estudiantes hacen que la enseñanza de las matemáticas se replantea de una manera positiva. Es así, que los docentes que participaron en el proceso reconocen que es necesario una transformación en sus prácticas pedagógicas, con una mayor disposición a los nuevos modelos y estrategias con el fin de que los estudiantes comprendan esta área importante de las ciencias, es ahí donde deben asumir los docentes su rol de mediador en el aprendizaje. Tal como lo plantean Black y William (1998), que resaltan el papel importante de las evaluaciones formativas, ya que permiten hacer un seguimiento y observación en el proceso de aprendizaje de los estudiantes, y ayudar a que el docente logre reflexionar y mejorar sus prácticas pedagógicas, enfocándolas más hacia el aprendizaje significativo y los diferentes contextos que devienen de cada estudiante.

En suma, este estudio aporta a la discusión sobre la igualdad en el aprendizaje teniendo en cuenta que, al aplicar un enfoque basado en la resolución de problemas reales, van de la mano con una planificación pedagógica, que puede ofrecer oportunidades de aprendizajes para equitativas, desensañadas para todos los estudiantes. En el caso de esta investigación para los participantes, el modelo hizo posible que entendieran y aprendieran conceptos complejos, reconociendo sus realidades para darle un nuevo significado a la escuela y sus procesos de aprendizaje. Esto no solo evidencia una mejora en el rendimiento académico, sino también una transformación en al aprendizaje de los estudiantes y las realidades que se viven en el contexto escolar. El Aprendizaje Basado en Problemas y la estructura multiplicativa, muestran que se pueden lograr aprendizajes significativos, que puedan motivar a través de las realidades y sus entornos.

CONCLUSIÓN

En conclusión, los hallazgos que se obtuvieron en esta investigación permiten ver que al implementar un modelo didáctico basado en el Aprendizaje Basado en Problemas (ABP), con la estructura multiplicativa, deja un impacto positivo y de gran significancia en el rendimiento académico de los estudiantes de grado quinto de instituciones públicas de la ciudad de Barranquilla, en el área de matemáticas. Esta metodología además de mejorar los niveles de desempeño en las pruebas que se aplicaron, promovió también un cambio en la actitud de los estudiantes con una más activa, reflexiva y colaborativa. Además de que, esto ayudó al desarrollo de las habilidades matemáticas que son fundamentales a través de la contextualización de los contenidos, la resolución de problemas y el trabajo cooperativo. Dichas estrategias fueron de gran relevancia para que los estudiantes lograran interpretar y aplicar la multiplicación desde una perspectiva más profunda y analítica.

Por otro lado, desde el punto de vista pedagógico, esta investigación revela que existe la posibilidad de poder transformar las prácticas docentes tradicionales a unas más en función de las necesidades de los estudiantes y del contexto, a través de estrategias que activas y centradas en que los docentes sean una guía del aprendizaje de todos los alumnos en un aula de clases. Los docentes que participaron en este estudio demostraron un mayor interés por la enseñanza, una planificación más intencionada con un actitud y pensamiento más abierto hacia las nuevas metodologías. Además, que la evaluación formativa tuvo un papel muy importante en el seguimiento del proceso estudiantil, permitiendo que los docentes le hicieran los ajustes necesarios y constantes en la intervención.

Se permite afirma, que este tipo de propuestas tienen un gran potencial para ser replicadas en contextos educativos vulnerables, donde existe la desigualdad, la falta de recursos y el bajo rendimiento académico. Tal como se observó en las instituciones educativas que fueron objeto de estudio en la ciudad de Barranquilla, teniendo en cuenta una planificación enfocada a una didáctica bien estructurada centrada en el contexto y la resolución de problemas reales y cotidianos que puedan generar un cambio y transformación, independiente del escenario en al que se dé.

En resumen, el modelo didáctico que se aplicó fue de gran ayuda para el mejoramiento del rendimiento académico en el área de matemáticas y ayudó a fortalecer los procesos dados en el contexto escolar, llenado a los estudiantes a ser más críticos y conscientes de su entorno, sabiendo que las ciencias pueden ser aplicadas a cualquier contexto. Lo que insta a los futuros investigadores sobre el tema a seguir indagando e innovando en la enseñanza de las matemáticas, haciendo que los enfoques de esta reconozcan la diversidad de la población estudiantil, y sea capaz de adaptarse al currículo con una visión abierta de poder transformar la enseñanza fuera y dentro de las instituciones.

REFERENCIAS

Barrows, H. S. (1986). A taxonomy of problem‑based learning methods. Medical Education, 20(6), 481–486.

Black, P., & Wiliam, D. (1998). Inside the Black Box: Raising Standards Through Classroom Assessment. Phi Delta Kappan, 80(2), 139–148.

Calle‑Bermeo, Y. A., García‑Herrera, D. G., Mena‑Clerque, S. E., & Erazo‑Álvarez, J. C. (2020). Aprendizaje basado en problemas y trabajo colaborativo para la enseñanza de matemática. Episteme Koinonia: Revista Electrónica de Ciencias de la Educación, Humanidades, Artes y Bellas Artes, 3(1), 436–458. https://doi.org/10.35381/e.k.v3i1.1019

García Jiménez, S. (2020). Diseño y análisis en la investigación educativa cuantitativa. Editorial Síntesis.

Hernández Sampieri, R., Fernández Collado, C., & Baptista Lucio, P. (2014). Metodología de la investigación (6.ª ed.). McGraw‑Hill.

Hernández-Sampieri, R., & Mendoza, C. P. (2018). Metodología de la Investigación: Las rutas cuantitativa, cualitativa y mixta (Impreso por Edamsa Impresiones ed.). (I. E. C.V, Ed.) México D.F: Ma Graw Hill - Interamericana Editores S.A de C.V.

Hmelo‑Silver, C. E. (2004). Problem‑Based Learning: What and How Do Students Learn? Educational Psychology Review, 16(3), 235–266.

Hurtado de Barrera, J. (2010). Metodología de la investigación holística (6.ª ed.). Fundación Sypal.

Pólya, G. (1945/1957). How to Solve It: A New Aspect of Mathematical Method. Princeton University Press.

Strobel, J., & van Barneveld, A. (2009). When is PBL more effective? A meta-synthesis of meta-analyses comparing PBL to conventional classrooms. Interdisciplinary Journal of Problem-Based Learning, 3(1), 44–58. https://doi.org/10.7771/1541-5015.1046

Vergnaud, G. (1996). Multiplicative conceptual field: what and why? En H. Guershon & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 41–60). SUNY Press..