La teoría de Schrödinger en la Resolución de Problemas en un Modelo por Competencias en Educación Superior

Schrödinger's Theory of Problem Solving in a Competency-Based Model in Higher Education

Xochil María Torrez Silva¹, José de la Cruz Cruz-Cruz² y Cliffor Jerry Herrera Castrillo³

¹Universidad Nacional Autónoma de Nicaragua, Managua, Centro Universitario, Estelí, Nicaragua, txmaria.silva@gmail.com, https://orcid.org/0000-0002-8158-4874, Nicaragua

²Universidad Nacional Autónoma de Nicaragua, Managua, Centro Universitario, Estelí, Nicaragua, jc4978405@gmail.com, https://orcid.org/0000-0001-7646-5187, Nicaragua

³Universidad Nacional Autónoma de Nicaragua, Managua, Centro Universitario, Estelí, Nicaragua, cliffor.herrera@unan.edu.ni, https://orcid.org/0000-0002-7663-2499, Nicaragua

	Información del Artículo	RESUMEN
	Trazabilidad: Recibido 13-10-2024 Revisado 15-10-2024 Aceptado 31-10-2024	Este estudio se centra en la resolución de problemas utilizando Operadores Matemáticos aplicados a la Teoría de Schrödinger en la mecánica cuántica, con un enfoque por competencias para estudiantes de quinto año de la carrera Física-Matemática en la UNAN-Managua/CUR Estelí. El objetivo principal fue validar la eficacia de actividades didácticas que involucraran la aplicación de Operadores Matemáticos, como el Hamiltoniano, en problemas cuánticos complejos. Se utilizó una metodología cuantitativa y cualitativa, con análisis de pruebas teóricas, entrevistas y proyectos colaborativos entre los estudiantes. Los resultados demostraron que el enfoque por competencias facilitó una mayor comprensión y aplicación de los Operadores en la ecuación de Schrödinger, con un 70% de los estudiantes identificando correctamente los operadores clave y un 85% resolviendo problemas complejos de manera adecuada. Las conclusiones sugieren que esta metodología no solo mejora la capacidad de los estudiantes para resolver problemas, sino que también promueve un aprendizaje más profundo y aplicado de la física cuántica.
	Palabras Clave: Operadores matemáticos Teoría de Schrödinger Mecánica cuántica Enfoque por competencias Resolución de problemas
Keywords: Mathematical operators Schrödinger's theory Quantum mechanics Competency-based approach Problem solving		ABSTRACT This study focuses on problem solving using Mathematical Operators applied to Schrödinger's Theory in quantum mechanics, with a competency-based approach for fifth year students of Physics-Mathematics at UNAN-Managua/CUR Estelí. The main objective was to validate the effectiveness of didactic activities involving the application of Mathematical Operators, such as the Hamiltonian, in complex quantum problems. A quantitative and qualitative methodology was used, with analysis of theoretical evidence, interviews and collaborative projects among students. The results showed that the competency-based approach facilitated a greater understanding and application of the Operators in the Schrödinger equation, with 70% of the students correctly identifying the key operators and 85% solving complex problems adequately. The findings suggest that this methodology not only improves students' problem-solving skills, but also promotes deeper and more applied learning of quantum physics.

INTRODUCCIÓN

En este trabajo se propone una solución innovadora para la enseñanza de la resolución de problemas utilizando Operadores Matemáticos aplicados a la Teoría de Schrödinger en la Mecánica Cuántica, con un enfoque por competencias. Esta investigación se llevó a cabo con estudiantes de quinto año de la carrera de Física-Matemática en la UNAN-Managua/CUR Estelí. La Teoría de Schrödinger es un pilar fundamental en la Física Cuántica, pero su enseñanza presenta desafíos significativos debido a la complejidad Matemática que implica. En este contexto, el enfoque por competencias busca no solo que los estudiantes adquieran conocimiento teórico, sino también que desarrollen habilidades prácticas para la aplicación de operadores como el Hamiltoniano y el operador momento en la resolución de problemas reales. Esta investigación, al centrarse en un método didáctico activo y participativo, pretende mejorar el rendimiento académico y la capacidad de resolución de problemas de los estudiantes, contribuyendo al fortalecimiento de sus competencias profesionales en el campo de la física cuántica.

En el ámbito de la Física Cuántica, uno de los desafíos más significativos en la resolución de problemas es el uso y comprensión de los Operadores Matemáticos. Estos operadores son fundamentales para describir y predecir el comportamiento de partículas a nivel subatómico, y su correcta aplicación es crucial para la formulación y resolución de ecuaciones cuánticas. Sin embargo, la complejidad inherente a estos operadores, junto con la naturaleza abstracta de la Teoría de Schrödinger, presenta dificultades considerables para estudiantes e investigadores (Vitaly, 2022; Herrera-Castrillo, 2024)

Una de las principales dificultades radica en la disponibilidad limitada de material didáctico que aborde estos temas de manera accesible y comprensible. A menudo, los recursos educativos existentes se centran en aspectos más generales de la Mecánica Cuántica, dejando un vacío en la enseñanza específica de los operadores matemáticos y su implementación práctica. Esta carencia puede limitar la capacidad de los estudiantes para dominar conceptos avanzados y aplicar eficazmente las herramientas matemáticas necesarias para la resolución de problemas complejos.

Además, la Teoría de Schrödinger, que es central para la descripción del comportamiento de sistemas cuánticos, requiere una comprensión profunda de cómo los operadores matemáticos interactúan con las funciones de onda y otros elementos fundamentales (Sarriugarte, 2023). La falta de recursos adecuados puede dificultar la capacidad de los investigadores para desarrollar nuevas técnicas o mejorar las existentes en el análisis de sistemas cuánticos.

Por lo tanto, el desafío no solo está en la comprensión teórica de los operadores matemáticos, sino también en la aplicación práctica de estos conceptos en problemas cuánticos reales (Morales-Espinoza et al., 2024). Para superar estas dificultades, es esencial desarrollar y proporcionar material didáctico específico que aborde la Teoría de Schrödinger y la aplicación de operadores matemáticos de manera más detallada y accesible. Esto permitirá a los estudiantes e investigadores mejorar su competencia en el campo y avanzar en la resolución de problemas complejos en la Física Cuántica.

La ecuación se considera un desafío Matemático debido a la cantidad de conocimientos algebraicos, científicos y prácticos que requiere. En el campo de la Física, muchos problemas requieren el uso de Operadores Matemáticos como aplicaciones entre funciones que representan estados físicos. (Pardos Cardiel, 2022; Herrera-Castrillo, 2023; Gómez-Martínez et al., 2024;)

Se han realizado varios estudios, a nivel internacional, que contribuyen al avance en la aplicación de las matemáticas en la Física y en la enseñanza de la Mecánica Cuántica. Pardos (2022) desarrolló una investigación centrada en la simulación de operadores matemáticos mediante redes neuronales, concluyendo que estas redes son capaces de aprender y predecir la actuación de dichos operadores en el contexto de la Física. González (2022), por su parte, investigó el enfoque matemático necesario para comprender la Mecánica Cuántica, proporcionando una base teórica esencial para futuras investigaciones en el campo. Finalmente, Córdoba-Fuentes y Herrera-Castrillo (2024) analizaron las consistencias e inconsistencias del famoso experimento del gato de Schrödinger, señalando que ciertos aspectos de la teoría cuántica pueden coincidir con la mecánica clásica y el sentido común, lo que resulta fundamental en la formación de futuros profesionales en tecnologías cuánticas.

A nivel nacional, se carecen de estudio sobre la resolución de problemas de Física Cuántica. las investigaciones más frecuentemente abordadas en Nicaragua son sobre estrategias metodológicas en temáticas sobre óptica, termodinámica, electricidad, electromagnetismo y física básica, dejando de lado los temas concernientes a Física Moderna, por ser considerados abstractos. Sin embargo, algunos trabajos de tesis doctorales y artículos científicos y ensayos, hacen referencia a la importancia de la Física Cuántica y el nivel matemático que se debe poseer para compresión y análisis físico (Castillo-Castillo et al., 2023). Algunos estudios que se utilizaron en este artículo, por su cercanía con la Física y la resolución de problemas en un modelo por competencias son:

Herrera (2022) desarrolló una metodología para el aprendizaje por competencias en Física Matemática mediante tecnología, destacando cómo los docentes, a nivel básico, utilizan recursos tecnológicos para mejorar el aprendizaje. González (2022) abordó las estrategias exitosas de aprendizaje en la educación a distancia, destacando la importancia de la motivación intrínseca generada por el reconocimiento de los logros estudiantiles. Ponce et al. (2023) investigaron la implementación de la integral definida en el análisis de la viscosidad de fluidos, integrando matemáticas y ciencia para fomentar el pensamiento crítico. López et al. (2023) aplicaron el cálculo integral en la compresibilidad de fluidos en un campo vectorial, demostrando la importancia de la evaluación informada para la progresión del aprendizaje. Estos estudios resaltan la relevancia de enfoques innovadores y multidisciplinarios en la enseñanza y el análisis de fenómenos complejos, promoviendo una comprensión más profunda y crítica en cada área.

Para realizar un estudio profundo de la Mecánica Cuántica, es fundamental que la teoría esté sólidamente cimentada mediante definiciones matemáticas y postulados físicos bien establecidos. Estos han sido comprobados y aceptados a lo largo de la historia por una amplia comunidad científica (Leija & Leija, 2021)

La teoría está sólidamente fundamentada en definiciones matemáticas y postulados físicos firmemente establecidos. Estos principios son analizados por los estudiantes de V año de la carrera de Física y Matemáticas en la UNAN-Managua/CUR-Estelí. La validación de este marco teórico por parte del personal científico, con una base conceptual robusta, es esencial para el desarrollo y el estudio riguroso de la mecánica cuántica. Solo con estos fundamentos teóricos y metodológicos bien consolidados, los estudiantes podrán avanzar de manera sistemática en la comprensión y aplicación de los fenómenos de la Física Cuántica (Valeriano, 2024).

Algunos conceptos, claves para este estudio son el de enfoque por competencias o aprendizaje basado en competencias, es una metodología educativa cuyo fundamento es el facilitar que los alumnos adquieran los contenidos de cada materia a través de situaciones prácticas y entornos experimentales. Este sistema, por lo tanto, se contrapone a los modelos clásicos de educación en los que se expone un temario de manera eminentemente teórica y los alumnos han de memorizar los datos para luego ser evaluados (Torres, 2024; Briones y Herrera-Castrillo, 2024).

También, los operadores matemáticos siempre van a ser símbolos matemáticos, cuando van cada uno sin ningún acompañamiento, obviamente, no tienen ningún significado, en cambio, cuanto está acompañado por una ley deformación, esto recobra su relevancia (Huzco, 2021; Rodríguez et al., 2024)

La ecuación de Schrödinger proporcionará la ayuda necesaria. Esta es la ecuación que establece la forma de la función de onda Ψ (x,t (i)), que actúa sobre la partícula asociada especificando la energía potencial que corresponde a dicha fuerza. En otras palabras, la función de onda es una solución a la ecuación de Schrödinger para la energía potencial. El tipo más común que tiene como solución una función es una ecuación diferencial. De hecho, la ecuación de Schrödinger es una ecuación diferencial. Esto es, la ecuación es una relación entre su solución Ψ (x,t), y ciertas derivadas de Ψ(x,t), con respecto a la variable independiente de espacio y tiempo 𝑥 y 𝑡. Como hay más de una variable independiente, las derivadas deberán ser derivadas parciales, tal como se muestra en la figura 1

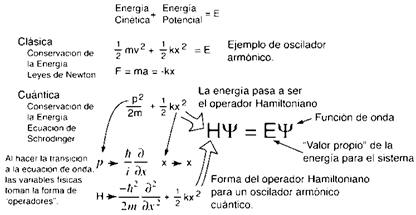
Fig. 1: Ecuación de Scrhödinger y su significado (Eisberg, 1979)

Sea la ecuación del Schrödinger propuesto por el físico austriaco Erwin Scrhödinger en 1925

(1)

Como indican Ayala y Rojas (2021) el dato inicial , donde s es un número real y se denota  al espacio de Sobolevperiódico de ordens. Dicha ecuación describe la evolución temporal de una partícula no relativista. Esta ecuación es importante en la teoría de la mecánica cuántica. Schrödinger discute en detalle lasrelaciones entre la mecánica hamiltoniana y óptica en 1926

El objetivo de este artículo es validar actividades con problemas con Operadores Matemáticos aplicados en Física Cuántica con enfoque por competencia con estudiantes de V año de Física Matemática de la UNAN-Managua/CUR-Estelí, siendo la hipótesis del trabajo:

"Si los estudiantes de V año en la Carrera de Física-Matemática reciben una formación específica en la aplicación de Operadores Matemáticos en la resolución de problemas de la Teoría de Schrödinger de la Mecánica Cuántica, entonces su capacidad para resolver problemas complejos relacionados con la mecánica cuántica mejorará significativamente en comparación con aquellos que solo reciben formación teórica general"

MATERIALES Y MÉTODOS

Paradigma de Investigación

Según Arias (2023), el pragmatismo, como paradigma de investigación y base epistemológica para los enfoques mixtos, se centra en la interrelación entre metodología, epistemología y métodos. Este paradigma se caracteriza por su énfasis en la acción, la utilidad, la adaptabilidad metodológica y la orientación hacia la solución de problemas específicos dentro del contexto educativo.

Tipo de investigación

Para el desarrollo del presente estudio se utilizó el enfoque mixto. Tal como expresa Medina et al. “es una vinculación de elementos de los métodos cuantitativo y cualitativo. La idea fundamental de este enfoque es tomar en cuenta las fortalezas de ambos métodos para obtener una comprensión más completa y enriquecedora de los fenómenos estudiados” (2023, p. 16).

La investigación realizada es de tipo descriptiva, ya que busca detallar aspectos importantes sobre las variables o individuos sometidos a análisis. El objetivo de este tipo de investigación es establecer una descripción lo más completa posible de un fenómeno, situación o elemento concreto, sin buscar causas ni consecuencias. Se mide las características y se observa la configuración y los procesos que componen los fenómenos, sin detenerse a valorarlos (Salamanca, 2018).

De acuerdo con las variables proporcionadas en este estudio, la investigación es no experimental. Según Ochoa y Landero, “el investigador no manipula variables independientes, sino que observa y analiza el fenómeno en su contexto natural para obtener información” (2021, p. 2).

Este tipo de investigación, según el tiempo de realización, es transversal, ya que se desarrolla en un periodo específico, precisamente para la observación, aplicación de instrumentos de recolección de datos. Según Cvetkovic-Vega et al. (2021), los estudios transversales ofrecen una forma rápida y económica de evaluar la prevalencia de una condición y examinar las asociaciones entre exposiciones y resultados. Sin embargo, la relación temporal entre exposición y efecto se mide simultáneamente en un solo período de tiempo.

Área geográfica

Se tomó como punto geográfico UNAN-Managua, CUR-Estelí, porque esta institución universitaria permite la accesibilidad de la realización de trabajos educativos. Está universidad está situada en el barrio 14 de abril al noroeste de la ciudad de Estelí (Barreda et al., 2024).

Población y muestra

La población de esta investigación se refiere al conjunto total de estudiantes inscritos en la carrera de Física-Matemática de la UNAN-Managua/CUR-Estelí. Esta población incluye a todos los estudiantes desde el primer año hasta el quinto año de la carrera. Es decir, abarca a todos los estudiantes actualmente matriculados y que están cursando cualquiera de los cinco años del programa académico de Física Matemática.

Tabla 1: Población de estudiantes

I Año	II Año	III Año	IV Año	V Año
34	13	20	17	31

Como afirma Condori (2020) la muestra es una parte representativa de la población que comparte las mismas características generales que esta. En el caso de este estudio se trabajará con estudiantes de la carrera de Física Matemática, se tomará el plan de estudio:

· Plan 2021 enfoque por competencias

Para lograr esto, se toma de muestra los 30 estudiantes de V año de Física Matemática que reciban el componente Física Cuántica durante el segundo semestre 2024. Además 7 docentes de Física-Matemática.

Al ser una investigación de tipo mixta, el muestreo es no probabilístico. según Cortes et al. (2023) el muestreo es no probabilístico, pero implica obtener muestras donde no todos los individuos de la población tienen las mismas posibilidades de ser seleccionados. Esto ocurre generalmente cuando acceder a una muestra probabilística es económica o técnicamente inviable. Es importante tener en cuenta que la muestra obtenida no es representativa y se selecciona según ciertos criterios específicos.

Como afirma Hernández y Carpio (2019) en los métodos no probabilísticos, los sujetos se seleccionan cuidadosamente de la población utilizando ciertos criterios, buscando ser los más representativos posibles. Aun así, no se utilizan para inferir resultados respecto de la población.

Muestreo por conveniencia:

Según Hernández (2021) la selección de la muestra se basa en la conveniencia del investigador, lo que le permite elegir de forma arbitraria la cantidad de participantes que pueden formar parte del estudio. Por tanto, esta investigación tiene un tipo de muestreo no probabilístico dado que los estudiantes fueron elegidos por conveniencia.

Muestreo de Expertos:

Según Reales et al. (2022) el muestreo de expertos es una forma de selección intencionada que se emplea para consultar a individuos con conocimientos especializados. Este enfoque puede ser crucial en la etapa inicial de la investigación cualitativa, ya que ayuda a identificar áreas potencialmente nuevas de interés.

Etapas de la investigación

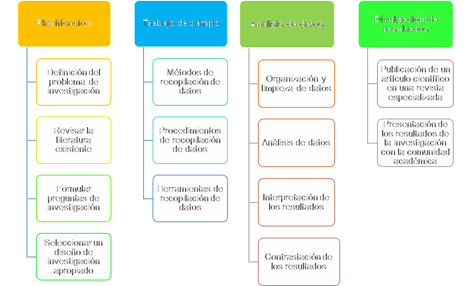
Fig. 2: Etapas que se siguieron en el proceso de investigación

RESULTADOS Y DISCUSIÓN

En este apartado se realiza un análisis de los resultados obtenidos a través de los instrumentos aplicados la Analizar problemas con Operadores Matemáticos aplicados en Física Cuántica con enfoque por competencia con estudiantes de V año de Física Matemática, de la Universidad Nacional Autónoma de Nicaragua, UNAN Managua, Centro Universitario CUR Estelí. para la recolección de datos a los estudiantes de V año de la carrera de Física-Matemática. Se utilizarán herramientas como Excel, SPSS, Jamovi. Este análisis tendrá una triangulación de los datos entre los objetivos de la investigación, los fundamentos teóricos, los antecedentes y los resultados obtenidos.

Adaptar problema con Operadores Matemáticos

Para hacer el análisis del primer objetivo de investigación que ajusta en adaptar problema de Operadores Matemáticos (como el Hamiltoniano, el operador momento y el operador de posición) aplicados en la Teoría de Schrödinger. Para evaluar grado de comprensión de los estudiantes se realizó una observación a través de pruebas teóricas y entrevistas semiestructuradas con el objetivo de analizar como perciben el alumno las fórmulas cuánticas, especialmente la ecuación de Schrödinger con operadores.

Para hacer la adaptación de problema se realizó una revisión bibliográfica en donde se revisó (libro de física cuántica) en este libro se realizó una interpretación de los ejercicios para tener un mayor análisis de la ecuación de onda, donde se puede constatar que los ejercicios son extractos, en donde se pudo revisar todos los problemas relacionados con la ecuación de Schrödinger.

Según la explicación de los ejercicios realizados en el libro de física cuántica, la ecuación de onda es fundamental para entender la dinámica de los sistemas cuánticos. A través de la revisión de los ejercicios, se puede observar cómo la ecuación de onda se aplica a diferentes problemas relacionados con la mecánica cuántica, lo que resalta su importancia en la comprensión de fenómenos físicos en escalas muy pequeñas.

La ecuación de onda, también conocida como la ecuación de Schrödinger, es un marco teórico que describe el comportamiento de un sistema cuántico en términos de una función ondulatoria. A través de la resolución de los ejercicios presentados en el libro, se puede ver cómo esta ecuación se aplica a problemas como la descomposición de sistemas cuánticos en componentes más simples, la interacción entre partículas cuánticas y la determinación de propiedades físicas de los sistemas en cuestión.

En resumen, la revisión de los ejercicios realizados en el libro de física cuántica muestra la importancia de la ecuación de onda en la comprensión de la mecánica cuántica, y su aplicación en problemas relacionados con la descomposición de sistemas cuánticos, la interacción entre partículas cuánticas y la determinación de propiedades físicas (López et al., 2023).

Se llevó a cabo una revisión exhaustiva sobre artículos relacionados con la ecuación de Schrödinger con el objetivo de profundizar en la comprensión de su fórmula. Este estudio no solo permitió un mejor dominio teórico, sino que también facilitó la selección de ejercicios adecuados que involucraran operadores matemáticos. Al entender más a fondo los conceptos subyacentes, se logró aplicar este conocimiento en problemas prácticos, enriqueciendo así el aprendizaje y la capacidad de resolución de problemas en el ámbito de la mecánica cuántica.

Los resultados indicaron que el 70% de los estudiantes logró identificar correctamente los principales operadores aplicados en la ecuación de Schrödinger, destacando el Hamiltoniano como el Operador clave para describir la energía total de un sistema Cuántico, lo que coincide con el estudio de González (2022).

Para un análisis detallado La ecuación de Schrödinger se considera un desafío Matemático debido a la cantidad de conocimientos algebraicos, científicos y prácticos que requiere. En el campo de la Física, muchos problemas requieren el uso de Operadores Matemáticos como aplicaciones entre funciones que representan estados físicos. (Pardos, 2022).

Al analizar el estudio de González (2022) se enfoca en destacar la importancia de la matemática en la comprensión de la mecánica cuántica, y cómo la aplicación de conceptos matemáticos puede proporcionar una comprensión más profunda y detallada de los fenómenos físicos. A través de este análisis, se busca proporcionar un marco de referencia para aquellos que buscan entender los principios fundamentales de la mecánica cuántica y su aplicación en diferentes áreas de la física.

En palabras de Huzco (2021) destaca la importancia de los operadores matemáticos en la mecánica cuántica, destacando que, sin una ley de deformación o una ecuación asociada, estos operadores no tienen ningún significado. Sin embargo, cuando están acompañados por una ley de deformación o una ecuación, los operadores matemáticos recobran su relevancia y se convierten en herramientas fundamentales para describir el comportamiento de los sistemas cuánticos.

En este trabajo se puede apreciar el análisis de la Física Cuántica que representa el estudio de la ecuación onda-partícula, la función de onda colapsa y la partícula se manifiesta como una entidad puntual en cuanto a partícula son los comportamientos ondulatorios asociados que describe su probabilidad de existir en diferentes posiciones.

En palabras de López et al. (2023) destaca la importancia de abordar la enseñanza de ecuaciones diferenciales de manera efectiva, teniendo en cuenta las necesidades y habilidades de los estudiantes. Se requiere un enfoque más personalizado y adaptativo, que tenga en cuenta la complejidad y el ritmo de aprendizaje de cada estudiante, para evitar la frustración y el desánimo, y para promover un aprendizaje más armónico y efectivo.

En palabras de Torres (2024) El enfoque por competencia es un sistema educativo que ofrece varias ventajas frente al modelo tradicional, uno de los principales beneficios es que reduce la cascada de datos y el efecto bola de nieve que se produce en el modelo tradicional. En este sentido, el enfoque por competencia promueve un aprendizaje más individualizado y personalizado, donde los estudiantes trabajan en equipo y compiten entre sí de manera constructiva.

En resumen, la cita de Leija y Leija (2021) destaca la importancia de la teoría de la mecánica cuántica, subrayando que su aceptación y verificación han sido comprobadas y ratificadas por una amplia comunidad científica. La base de esta teoría se encuentra en definiciones matemáticas y postulados físicos bien establecidos, que han sido desarrollados y refinados a lo largo de la historia.

Se llevó a cabo una entrevista con un docente que expresó su opinión sobre la adaptación de problemas en la educación, considerándola un gran desafío debido a su gran complejidad. Según el docente, estos problemas pueden ser particularmente difíciles de resolver, lo que lleva a utilizar operadores matemáticos para simplificar y reducir su complejidad.

Es importante revisar y buscar ejercicios de menor complejidad relacionados con la materia, ya que estos pueden ser una herramienta valiosa para ayudar a los estudiantes a comprender y resolver problemas más complejos. Los ejercicios de menor complejidad pueden servir como una base para el desarrollo de métodos factibles y efectivos para resolver problemas más complejos, lo que puede hacer que la resolución de estos problemas sea más accesible y entendible para los estudiantes.

Asimismo, se puede crear la capacidad de analizar, de observar información ya sé dé libros o revista que permitiera una mayor comprensión del ejercicio de dicha temática y así logren encontrar adecuadamente los operadores en la ecuación de Schrödinger, mostrando así una mejora significativa en la adaptación y resolución de problema.

Se pudo analizar el manejo de las matemáticas que se necesitan aplicar muchas fórmulas signos y creatividad para desarrollar los diferentes ejercicios, en tal sentido, para resolver algunos problemas matemáticos o aritméticos se requiere de símbolos matemáticos especiales a fin de realizar las operaciones con éxito. (Huzco, 2021).

Esto ocurre cuando un alumno tiene problemas para comprender un punto muy concreto de la lección y esto supone que no asimile correctamente todo lo que viene después, pues se trata de una cuestión acumulativa. Esto supone frustración y pérdida de interés (Torres, 2024).

El éxito en la adaptación de los Operadores se atribuye al enfoque por competencias implementado en el curso. Las estrategias empleadas, tales como el uso de problemas aplicados y simulaciones numéricas, permitieron que los estudiantes no solo memorizaran las definiciones, sino que también pudieran comprender su aplicación en la resolución de problemas reales.

El análisis de los datos, que incluyó las pruebas teóricas, las entrevistas con expertos docentes y las observaciones en el aula, mostró una coherencia general en las conclusiones obtenidas. De manera consistente, tanto los estudiantes como los docentes expresaron su acuerdo con que la metodología basada en competencias había mejorado significativamente la capacidad de los estudiantes para adaptar Operadores en diferentes contextos físicos. Esta coherencia sugiere que la implementación de esta metodología ha tenido un impacto positivo en la comprensión y aplicación de los Operadores en la Física Cuántica.

De acuerdo los estudios previos de Pardos (2022), se destaca la importancia de enfoques prácticos y aplicados en la enseñanza de la Física Cuántica. Al analizar estos estudios, se confirma que la comprensión de los Operadores se consolida cuando se contextualiza el aprendizaje dentro de problemas reales. Este enfoque no solo ayuda a mejorar la comprensión de los conceptos, sino que también fomenta una mejor retención y aplicación del conocimiento. Al resolver problemas prácticos y relevantes, los estudiantes desarrollan una comprensión más profunda y significativa de los Operadores y su papel en la Física Cuántica.

Se analizo también esta fuente Eisberg (2023), la teoría de Schrödinger se desarrolla como un marco para tratar sistemas microscópicos importantes, como el átomo, cuyo estudio ha revelado la base de la química y de la física del estado sólido.

En este sentido, la teoría de Schrödinger proporciona una comprensión detallada de las propiedades del átomo, que están íntimamente relacionadas con las propiedades del núcleo. La teoría de Schrödinger es una de las herramientas fundamentales de la mecánica cuántica, y su comprensión es esencial para entender los fenómenos microscópicos que subyacen a la química y a la física del estado sólido.

En este trabajo, se utilizará la teoría de Schrödinger para tratar un sistema microscópico importante, y se explorarán los puntos esenciales de la teoría, con el fin de comprender mejor los fenómenos que se producen en el nivel microscópico.

Aplica el problema con Operadores.

Para dar salida al segundo objetivo se aplica una guía de aprendizaje, que se desarrolla con antecedentes experimentales de la teoría de Scrhödinger. Esto se llevó a cabo con estudiantes de V año de la carrera de física-Matemática de la UNAN- Managua-CUR-Estelí en el segundo semestre del 2024.con el fin, se llevó a cabo una lista de cotejo que permitió identificar la importancia de analizar y comprender los conceptos relacionados con la teoría de Scrhödinger física cuántica, así con la certeza de que la guía es viable en el proceso de aprendizaje.

Al iniciar la aplicación de la metodología basada en competencias, se implementó la primera asignación práctica para evaluar el conocimiento previo de los estudiantes sobre la ecuación de Schrödinger. En este paso, se llevó a cabo un completo de información donde los estudiantes debían llenar los espacios con palabras o frases que describieran la ecuación de Schrödinger. Esta actividad permitió observar cómo los estudiantes trabajaban en equipo, revisaban la información y verificaban que las palabras estuvieran correctas, lo que proporcionó una visión clara de sus habilidades en el manejo de la información y su capacidad para trabajar en equipo.

Esta observación fue crucial para identificar las fortalezas y debilidades de los estudiantes y para ajustar la metodología según sea necesario. Al analizar el resultado de la asignación práctica, se pudo determinar si los estudiantes tenían un conocimiento previo sólido de la ecuación de Schrödinger y si estaban capaces de aplicarla de manera efectiva. Esta información se utilizó como base para diseñar futuras actividades y para evaluar el progreso de los estudiantes en el aprendizaje de la ecuación de Schrödinger.

Ya desarrollando la aplicación de problemas, se les pidió a los estudiantes como segunda actividad, que eligieran un problema con operadores matemático específicos, donde se aplica la ecuación de Schrödinger dependiente del tiempo y del espacio. Se observó que un porcentaje de estudiantes no tuvieron dificultad con la selección adecuadamente de problemas relacionados con partículas en potenciales simples, como el pozo de potencial y la partícula libre.

Los estudiantes mostraron un interés adecuado y una comprensión sólida al resolver problemas de manera individual que requieren la aplicación de los Operadores, así como la evaluación del comportamiento físico del sistema cuántico. Su capacidad para analizar y resolver estos problemas demostró una comprensión genuina de los conceptos teóricos subyacentes, lo que es fundamental para avanzar en la comprensión de la mecánica cuántica.

El enfoque por competencias fue clave para que los estudiantes aplicaran problemas con operadores matemáticos que les permitieran aplicar sus conocimientos de forma crítica. A través actividades en equipo, los estudiantes aprendieron a identificar qué problemas podían ser mejor resueltos, utilizando Operadores matemático y cómo estos interactúan con las funciones de onda en diferentes contextos.

A partir de la evaluación de los trabajos grupales, las observaciones de aula y los comentarios del docente, se constató que aquellos estudiantes que participaron activamente en la selección y aplicación de problemas, lograron desarrollar un enfoque analítico más estructurado y eficiente en la resolución de los mismos. Esto implicó una mayor capacidad para analizar y resolver problemas de manera efectiva, lo que se reflejó en su desempeño en la resolución de la ecuación de Schrödinger.

A través de este análisis, se pudo evaluar la importancia de permitir que los estudiantes aplicaran problemas relevantes para su nivel de competencia y comprensión, lo que respalda la teoría del aprendizaje autodirigido en educación. La aplicación de problemas relevantes es fundamental para que los estudiantes puedan desarrollar una comprensión profunda de los conceptos y habilidades necesarias para resolverlos, lo que se convierte en una mejor retención y aplicación del conocimiento.

Estas averiguaciones concuerdan con investigaciones internacionales que han demostrado que el proceso de selección de problemas es una habilidad clave en la enseñanza de la Física Cuántica. La capacidad de seleccionar y aplicar problemas relevantes es esencial para que los estudiantes puedan desarrollar una comprensión profunda de los conceptos y habilidades necesarias para resolverlos, lo que se refleja en un mejor desempeño en la resolución de problemas.

El aprendizaje incluye cambios en el carácter o las habilidades de una persona que son relativamente permanentes y no se atribuyen únicamente a los procesos de desarrollo. El aprendizaje es un cambio relativamente permanente en el comportamiento generado por la experiencia.

En palabras de González (2023) El principal objetivo de este estudio fue analizar las estrategias exitosas de aprendizaje usadas por estudiantes universitarios. Para el desarrollo del tema que facilite la recuperación de lo aprendido, expresado con la elaboración, y asociado con la retroalimentación positiva por logro, la cual genera la motivación intrínseca requerida para continuar aprendiendo. Fue una investigación.

El aprendizaje es el proceso a través del cual se adquieren y desarrollan habilidades, conocimientos, conductas y valores. Es resultado de la atención, el estudio, la experiencia, la instrucción, el razonamiento, la observación, así como la influencia de factores externos con los cuales interactuamos, existen muchos tipos de aprendizaje diferentes, en función por ejemplo de cuántas repeticiones son necesarias para adquirir la nueva información, o de cuál es el papel que juega el propio aprendiz en el proceso.

En general, como grupo investigador se puede concluir que la participación en la selección y aplicación de problemas fue clave para el desarrollo de un enfoque analítico más estructurado y eficiente en la resolución de problemas, lo que se convirtió en un mejor desempeño de los estudiantes en la resolución de la ecuación de Schrödinger.

CONCLUSIÓN

· Eficacia del Enfoque por Competencias: La aplicación del enfoque por competencias en la enseñanza de la Teoría de Schrödinger ha demostrado ser una metodología efectiva para mejorar la comprensión y aplicación de los operadores matemáticos en problemas complejos de mecánica cuántica. Los resultados indican que esta estrategia no solo facilita la resolución de problemas, sino que también promueve un aprendizaje más profundo, ayudando a los estudiantes a consolidar sus habilidades en física cuántica.

· Desarrollo de Habilidades Prácticas: A través de actividades didácticas que integran operadores matemáticos como el Hamiltoniano, los estudiantes han logrado mejorar sus habilidades prácticas, obteniendo una comprensión más integral de los conceptos y procesos subyacentes en la mecánica cuántica. Esto refleja la importancia de implementar metodologías activas que permitan a los estudiantes aplicar sus conocimientos en contextos reales y colaborativos.

· Contribución al Campo de la Física Cuántica: Este estudio contribuye al campo de la educación en física cuántica al proporcionar un modelo de enseñanza que enfatiza la relación entre teoría y práctica. La investigación valida el uso de operadores matemáticos en la resolución de problemas cuánticos complejos, destacando la utilidad de este enfoque para fomentar competencias fundamentales en los futuros profesionales de física.

· Impulso a la Innovación Educativa: La metodología empleada representa un avance hacia prácticas pedagógicas más innovadoras en la educación superior, especialmente en áreas de alta complejidad como la física cuántica. Este modelo de enseñanza, adaptable a otros contextos y disciplinas, ofrece un marco útil para futuras investigaciones que busquen mejorar la enseñanza de temas complejos mediante la integración de competencias prácticas.

· Aplicación de Operadores Matemáticos en Problemas Complejos: El uso de operadores matemáticos en el marco de la Teoría de Schrödinger ha permitido a los estudiantes abordar problemas complejos con mayor confianza y precisión, reflejando una mejor asimilación de la estructura y funcionalidad de dichos operadores. Este estudio subraya la relevancia de desarrollar material didáctico específico que facilite la comprensión y aplicación de conceptos avanzados en física cuántica.

· Recomendaciones para Futuros Estudios: Se sugiere realizar investigaciones adicionales que exploren la aplicabilidad de este modelo educativo en otros entornos de la educación superior, así como en áreas de estudio que requieran habilidades analíticas y prácticas avanzadas. Asimismo, es recomendable continuar desarrollando recursos educativos que hagan más accesibles estos contenidos a estudiantes con diferentes niveles de conocimiento previo en física y matemáticas.

REFERENCIAS

Arias Odón, F. (julio-diciembre de 2023). Paradigma pragmático como fundamento epistemológico de la investigación mixta. Revisión sistematizada. Educación, Arte, Comunicación: Revista Académica e Investigativa,, 12(2), 11-24. https://doi.org/10.54753/eac.v12i2.2020

Barreda Rodríguez, N. A., Peralta Calderón, Y. I., Farrach Úbeda, G. A., & Herrera Castrillo, C. J. (2024). Gestión de la calidad mediante la interrelación de los macroprocesos establecidos para la UNAN-Managua. Revista Multi-Ensayos, 10(20), 3-25. https://doi.org/10.5377/multiensayos.v10i20.18676

Briones Rugama, Y. Y., & Herrera-Castrillo, C. J. (2024). Desafíos en la enseñanza de la Geometría a nivel superior mediante enfoque por competencias. Wani Revista del Caribe Nicaragüense(81), 1-18. https://doi.org/10.5377/wani.v1i81.18461

Castillo-Castillo, K. I., Hernández-Meza, G. A., & Herrera-Castrillo, C. J. (2023). Estado del arte de investigaciones referente a Física Clásica y Moderna en el Período 2016 – 2021. Educación Superior, 22(35), 65–83. https://doi.org/10.56918/es.2023.i35.pp65-83

Condori Ojeda, P. (2020). Universo, población y muestra. Acta Académica. Obtenido de https://www.aacademica.org/cporfirio/18

Córdoba-Fuentes, D., & Herrera-Castrillo, C. (2024). Desarrollo de competencias en física-matemática a través de los productos integradores. Revista Científica ECOCIENCIA, 11(2), 24-43. https://doi.org/10.21855/ecociencia.112.875

Cortes Toledo, M., Moraga Álvarez, E., & Silva Jiménez, D. (2023). Técnicas de muestreo probabilístico para investigación en ciencias de la salud. ResearchGate, 13-23. https://www.researchgate.net/publication/374695823_TECNICAS_DE_MUESTREO_PROBABILISTICO_PARA_INVESTIGACION_EN_CIENCIAS_DE_LA_SALUD?enrichId=rgreq-fba78240e1724e42e12414f1bfd0eb76-XXX&enrichSource=Y292ZXJQYWdlOzM3NDY5NTgyMztBUzoxMTQzMTI4MTE5ODE3MDQ1MkAxNjk3

Cvetkovic-Vega, A., Maguiña, J. L., Soto, A., Lama-Valdivia, J., & Correa López, L. E. (2021). Estudios transversales. Revista de la Facultad de Medicina Humana, 21(1), 179-185. https://doi.org/10.25176/rfmh.v21i1.3069

Eisberg, R. (1979). Física Cuántica Átomos, Moléculas, Sólidos, Nucleos y Particulas. https://www.sidalc.net/search/Record/cat-unco-ar-59413/Description

Gómez-Martínez, K. N., Soriano-Sánchez, S. P., Soriano-Rivera, K. M., Triminio-Zavala, C. M., & Herrera-Castrillo, C. J. (2024). Guías de Laboratorio para el Aprendizaje del Electromagnetismo. Revista Latinoamericana de Calidad Educativa, 1(3), 11-20. https://doi.org/10.5281/zenodo.13630978

González Jaimes, E. I. (2023). Guía de enseñanza para el aprendizaje exitoso en educación a distancia universitaria. Universidad Autónoma del Estado de México, Mexico. https://doi.org/http://orcid.org/0000-0002-5328-5586

González Rojas, J. N. (2022). Un enfoque matemático de la mecania cuantica. Univercidad de panmplona, España. http://repositoriodspace.unipamplona.edu.co/jspui/handle/20.500.12744/3387

Hernández Ávila, C. E., & Carpio Escobar, N. A. (2019). Introducción a los tipos de muestreo. Revista científica Del Instituto Nacional De Salud, 2(1), 76-79. https://doi.org/10.5377/alerta.v2i1.7535

Hernández González, O. (2021). Aproximación a los distintos tipos de muestreo no probabilístico que existen. Revista Cubana de Medicina General integral, 37(3). http://www.revmgi.sld.cu/index.php/mgi/article/download/1442/453

Herrera Castrillo, C. J. (2022). Aprendizaje de ecuaciones diferenciales aplicadas en física utilizando tecnología. Revista Torreón Universitario, 7(31), 26–35. https://doi.org/10.5377/rtu.v11i31.14223

Herrera-Castrillo, C. J. (2023). Aplicaciones del Lenguaje de Categorías en diferentes actividades científicas y tecnológicas. Ciencia e Interculturalidad, 33(2), 187-204. https://doi.org/10.5377/rci.v33i2.17723

Herrera-Castrillo, C. J. (2024). Práctica pedagógica en mecánica relativista: enfoques, estrategias y su impacto educativo. Wani, 40(80), 4-22. https://doi.org/10.5377/wani.v40i80.17642

Huzco Puente, J. (2021). Operadores Matemáticos Para Desarrollar La Competencia Resuelve Problemas De Cantidad En Estudiantes. Univercidad Catilica Los Angeles Chimbote, Peru. https://repositorio.uladech.edu.pe/bitstream/handle/20.500.13032/26029/OPERADORES_MATEMATICOS_HUZCO_%20PUENTE_%20JENIFFER.pdf?sequence=1&isAllowed=y

Leija, I., & Leija, S. (2021). Contrucción Matemática de la educación de Schodinger. Universidad Autónoma de Nuevo León, Mexico. https://doi.org/https://www.researchgate.net/profile/Sao-Leija/publication/355038278_Construccion_Matematica_de_la_Ecuacion_de_Schrodinger/links/6159e70ca6fae644fbd084f9/Construccion-Matematica-de-la-Ecuacion-de-Schroedinger.pdf

López López, L. J., Rivera Díaz, R. E., Carrasco Sánchez, S. d., Medina Martínez, W. I., & Herrera Castrillo, C. J. (2023). Aplicaciones del cálculo integral en la compresibilidad de fluidos en un campo vectorial. Revista Ciencia E Interculturalidad, 32(1), 23-42. https://doi.org/10.5377/rci.v32i01.16232

Medina Romero, M. Á., Hurtado Tiza , D. R., Muñoz Murillo, J. P., Ochoa Cervantez, D. O., & Ordóñez, G. I. (2023). Método mixto de investigación: Cuantitativo y cualitativo. Instituto Universitario de Innovación Ciencia y Tecnología Inudi Perú. https://doi.org/10.35622/inudi.b.105

Morales-Espinoza, E. M., López-Acevedo, B. A., Moreno-Videa, D. J., & Herrera-Castrillo, C. J. (2024). Estrategias metodológicas para el aprendizaje del campo magnético en espiras circulares. Revista Latinoamericana de Calidad Educativa, 1(3), 37-49. https://doi.org/10.5281/zenodo.13841166

Ochoa Camacho, H., & Landero Gómez, D. d. (2021). Investigación experimental y no experimental. Maestría en Ciencias de la Salud en Formación en Docencia. https://salazarvirtual.sistemaeducativosalazar.mx/assets/6102aa6750ff4/tareas/9252cbda265c7f789a59cbc8557cc217investigacion%20experiemmntal.pdf

Pardos Cardiel, J. (2022). Operadores matemáticos en Física simulados mediante Inteligencia Artificial. [Tesis de Grado]. Universidad de Zaragoza. Obtenido de https://zaguan.unizar.es/record/125108/files/

Ponce Herrera, G., López Valdivia, F. S., Canales Urrutia, C. I., & Medina Martínez, W. I. (2023). Implementación de la integral definida para el análisis de la viscosidad de fluidos. Wani(79), 62–77. https://doi.org/10.5377/wani.v39i79.16921

Reales Chacón, L. J., Robalino Morales, G. E., Peñafiel Luna, A. C., Cárdenas Medina, J. H., & Cantuña-Vallejo, P. F. (octubre de 2022). El muestreo internacional no-probabilístico: herramienta de investigación científica en carreras de ciencias de la salud. Revista Universidad y Sociedad, 14(55), 681-691. https://rus.ucf.edu.cu/index.php/rus/article/download/3338/3278/

Rodríguez Diaz, J. E., Rivera González, E. M., Altamirano Vásquez, F. J., & Herrera Castrillo, C. J. (2024). Aplicación de integrales dobles y vectores en el cálculo de la densidad de circulación de fluidos. Uno Sapiens Boletín Científico De La Escuela Preparatoria No. 1, 7(13), 1-11. https://doi.org/10.29057/prepa1.v7i13.12307

Salamanca, V. (5 de febrero de 2018). MAC.INVESTIGACION. Obtenido de Metodología de la investigación: https://sites.google.com/site/macinvestigacion/tipos-investigacion#:~:text=Descriptiva,causas%20ni%20consecuencias%20de%20%C3%A9ste.

Santiago Ayala, Y., & Rojas Romero, S. (2021). Existencia y Regularidad de Solución de la Ecuación de Schrödinger no Homogénea en Espacios de Sobolev Periódico. Secciones Matemáticas, 8(1), 37-51. https://doi.org/10.17268/sel.mat.2021.01.04

Sarriugarte Gómez, I. (2023). La teoría del gato de Schrödinger y su trasladación artística. Revista de Humanidades, 1130-5029. https://openurl.ebsco.com/EPDB%3Agcd%3A12%3A26049980/detailv2?sid=ebsco%3Aplink%3Ascholar&id=ebsco%3Agcd%3A175928760&crl=c

Torres Tahua, D. M. (2024). La interrelación del enfoque por competencias y la retroalimentación en los educandos. Universidad Nacional José Faustino Sánchez Carrión, Peru. https://doi.org/https://repositorio.unjfsc.edu.pe/bitstream/handle/20.500.14067/8918/TESIS.pdf?sequence=1&isAllowed=y

Valeriano Meneses, M. A. (2024). El Enfoque STEM en la enseñanza de Electromagnetismo en un Programa de Formación Docente de la Universidad Técnica del Norte. Revista Latinoamericana de Calidad Educativa, 1(1), 33-38. https://doi.org/10.5281/zenodo.13151105

Vitaly, V. (2022). Una Dualidad Clásica-Cuántica y un Espacio-Tiempo Emergente. Obtenido de https://d1wqtxts1xzle7.cloudfront.net/111904821/Una_Dualidad_Cuantica_Clasica_y_un_Espacio_Tiempo_Emergente-libre.pdf?1709097503=&response-content-disposition=inline%3B+filename%3DUna_Dualidad_Clasica_Cuantica_y_un_Espac.pdf&Expires=1727941888&Signature=A