Influencia del uso de software de geometría dinámica en la comprensión conceptual de las cónicas en estudiantes de bachillerato

Influence of dynamic geometry software use on high school students’ conceptual understanding of conic sections

Carlos Rubén Zabala Villarreal¹, José Vicente Flores², Elena Elizabeth Pérez Muñoz³, Freddy Rolando Chicaz Taimal⁴, Paola Alejandra Vizcaíno Quiroz⁵ y Anderson Geovanny Cuamacás Ibujés⁶

¹Ministerio de educación, deporte y cultura, carlos.zabala@docentes.educacion.edu.ec, https://orcid.org/0009-0004-5700-5942, Ecuador

²Ministerio de educación, deporte y cultura, vicente.flores@docentes.educacion.edu.ec, https://orcid.org/0009-0008-1453-2637, Ecuador

³Ministerio de educación, deporte y cultura, elenae.perez@docentes.educacion.edu.ec, https://orcid.org/0009-0004-6790-1871, Ecuador

⁴Ministerio de educación, deporte y cultura, freddy.chicaz@docentes.educacion.gob.ec, https://orcid.org/0009-0007-8958-5998, Ecuador

⁵Ministerio de educación, deporte y cultura, paola.vizcaino@docentes.educacion.edu.ec, https://orcid.org/0009-0001-8387-2271, Ecuador

⁶Ministerio de educación, deporte y cultura, anderson.cuamacas@docentes.educacion.edu.ec, https://orcid.org/0009-0009-9949-0209, Ecuador

	Información del Artículo	RESUMEN
	Trazabilidad: Recibido 14-10-2025 Revisado 15-10-2025 Aceptado 16-11-2025	El presente estudio analiza el impacto del uso de software de geometría dinámica en la comprensión conceptual de las cónicas en estudiantes de bachillerato, la investigación se desarrolló bajo un enfoque cuantitativo con un diseño cuasiexperimental que incluyó un grupo control y un grupo experimental, ambos grupos realizaron un pretest para determinar su nivel inicial de conocimientos, evidenciándose una similitud en los puntajes que permitió establecer condiciones de comparación válidas, los resultados revelaron un incremento significativo en los puntajes del postest del grupo experimental en comparación con el grupo control, se observó una disminución en la variabilidad interna de los puntajes, lo que sugiere una comprensión conceptual uniforme entre los estudiantes que utilizaron la herramienta tecnológica; por otra parte, el análisis descriptivo confirmó la eficacia del software para favorecer el aprendizaje significativo de las cónicas. Se concluye que la integración de herramientas de geometría dinámica constituye una estrategia pedagógica efectiva para mejorar el rendimiento académico y fortalecer la comprensión conceptual en el estudio de las matemáticas a nivel de bachillerato. .
	Palabras Clave: Geometría dinámica Cónicas Comprensión conceptual Tecnologías educativas Aprendizaje significativo
Keywords: Dynamic Geometry Conic Sections Conceptual Understanding Educational Technologies Meaningful Learning		ABSTRACT The present study analyzes the impact of using dynamic geometry software on the conceptual understanding of conic sections among high school students. The research was conducted using a quantitative approach with a quasi-experimental design that included a control group and an experimental group. Both groups completed a pretest to determine their initial level of knowledge, revealing similarities in their scores that allowed for valid comparison conditions. The results showed a significant increase in the posttest scores of the experimental group compared to the control group. A decrease in the internal variability of the scores was also observed, suggesting a more uniform conceptual understanding among the students who used the technological tool. Furthermore, the descriptive analysis confirmed the effectiveness of the software in promoting meaningful learning of conic sections. It is concluded that the integration of dynamic geometry tools constitutes an effective pedagogical strategy for improving academic performance and strengthening conceptual understanding in the study of mathematics at the high school level.

INTRODUCCIÓN

La enseñanza de las matemáticas en el nivel de bachillerato enfrenta desafíos persistentes relacionados con la comprensión profunda de conceptos abstractos, entre estos, las cónicas, parábola, elipse e hipérbola, las cuales representan un conjunto de contenidos que suelen generar dificultades en los estudiantes debido a la necesidad de integrar representaciones geométricas, algebraicas y gráficas, la complejidad inherente a estos objetos matemáticos exige estrategias pedagógicas que favorezcan la visualización y la exploración dinámica para promover un aprendizaje significativo (Barallobres & Barallobres, 2016).

En este contexto, el uso de software de geometría dinámica (SGD) ha ganado relevancia en la última década como recurso clave para transformar la enseñanza tradicional de la geometría, aplicaciones como GeoGebra, Cabri Geometry o Desmos han demostrado ser herramientas poderosas para modelar y manipular construcciones geométricas de manera interactiva, su accesibilidad y capacidad para combinar múltiples representaciones convierten al SGD en una alternativa didáctica atractiva y efectiva para estudiantes y docentes (Enrique & Fernandez, 2020).

Estudios señalan que la visualización desempeña un rol fundamental en la comprensión conceptual de las matemáticas, La posibilidad de observar cómo un gráfico se modifica al alterar parámetros, o cómo las relaciones entre elementos geométricos se expresan dinámicamente, facilita la interiorización de propiedades y comportamientos matemáticos complejos, en el caso de las cónicas, esta visualización dinámica permite a los estudiantes establecer conexiones entre teoría y práctica, superando la limitación de las representaciones estáticas de los métodos tradicionales (López & Noguera, 2026).

El paradigma constructivista del aprendizaje destaca la importancia de la interacción activa con los objetos de estudio para promover la construcción del conocimiento, desde esta perspectiva, el SGD genera entornos de experimentación que permiten al estudiante formular conjeturas, verificar hipótesis y descubrir patrones por sí mismo, esta interacción significativa constituye una oportunidad para desarrollar habilidades de razonamiento geométrico y matemático que trascienden la simple memorización de fórmulas o procedimientos (Estrategia et al., 2022) .

En el ámbito del aprendizaje de las cónicas, el uso de SGD facilita el tránsito entre diferentes representaciones: algebraica, gráfica y geométrica, los estudiantes pueden manipular focos, directrices, radios y excentricidades, observando en tiempo real cómo interactúan estos elementos para definir una curva específica, esta experiencia directa promueve una comprensión más profunda y una apropiación conceptual que difícilmente se logra únicamente con explicaciones teóricas o ejercicios en papel (Rubio-Pizzorno & Espinosa, 2021).

La incorporación de tecnologías educativas en las aulas de bachillerato responde a la necesidad actual de integrar prácticas pedagógicas innovadoras que motiven a los estudiantes y fortalezcan sus competencias digitales, en particular, los SGD se alinean con los objetivos de educación matemática contemporánea al fomentar la autonomía, la exploración y la creatividad, estos factores contribuyen no solo al aprendizaje de contenidos específicos, sino también al desarrollo de capacidades transversales, como la resolución de problemas y el pensamiento crítico (Burgos-Macías et al., 2024) .

La implementación efectiva del SGD requiere reflexionar sobre aspectos pedagógicos y didácticos fundamentales, no basta con introducir tecnología en el aula; es necesario diseñar actividades que integren el software como mediador del aprendizaje, de forma que las interacciones con las herramientas digitales sean significativas y orientadas a objetivos claros, siendo así que el rol del docente debe adaptarse hacia una función más de guía o facilitador que de transmisor exclusivo de conocimiento (Palacios-Hidalgo & Cimas, 2024).

Las investigaciones recientes reportan mejoras tanto en el rendimiento académico como en la actitud hacia las matemáticas cuando se emplean SGD en el estudio de temas complejos como las cónicas, estas mejoras se atribuyen a la capacidad del software para ofrecer retroalimentación inmediata, permitir múltiples intentos exploratorios y favorecer una comprensión intuitiva basada en la manipulación directa de los objetos matemáticos, tales beneficios subrayan la necesidad de seguir estudiando el impacto real y las condiciones óptimas para integrar estos recursos en las aulas (Bozzano et al., 2020).

El presente artículo busca analizar el uso del software de geometría dinámica como herramienta para favorecer la comprensión conceptual de las cónicas en estudiantes de bachillerato, a través de una revisión detallada de estudios previos y del análisis teórico de sus implicaciones pedagógicas, se explora el potencial del SGD para transformar la enseñanza tradicional y promover un aprendizaje más significativo, interactivo y profundo.

MATERIALES Y MÉTODOS

El estudio se desarrolló bajo un enfoque cuantitativo, con el propósito de medir el efecto del uso de software de geometría dinámica en la comprensión conceptual de las cónicas en estudiantes de bachillerato, se empleó un diseño cuasi-experimental de tipo pretest–postest con grupo control, dado que los grupos ya estaban conformados de manera natural en la institución educativa participante, esta metodología permitió comparar el rendimiento académico entre estudiantes que utilizaron el software y aquellos que trabajaron con métodos tradicionales (Romero & Alvarado, 2025).

La población estuvo conformada por 120 estudiantes de segundo año de bachillerato, partir de esta población se seleccionó una muestra no probabilística intencional de 60 estudiantes distribuidos en dos grupos paralelos: un grupo experimental (n=30), que trabajó con software de geometría dinámica (GeoGebra), y un grupo control (n=30), que recibió instrucción tradicional basada en explicaciones magistrales y ejercicios en papel.

Los materiales empleados incluyeron computadoras portátiles o de laboratorio, acceso al software GeoGebra (versión clásica), cuadernos de ejercicios y una prueba estandarizada de comprensión conceptual sobre cónicas, diseñada por el equipo investigador, esta prueba fue validada mediante juicio de expertos en didáctica de la matemática y sometida a un análisis de confiabilidad interna mediante el coeficiente Alfa de Cronbach, obteniendo un valor de 0.89, lo cual indica alta consistencia interna.

El procedimiento se desarrolló durante un período de cuatro semanas.

Tabla 1: Diseño y Procedimiento de la Intervención

Fase	Semana	Grupo Control (GC)	Grupo Experimental (GE)	Objetivo de la Fase
I	1	Pre-test (Evaluación Inicial)	Pre-test (Evaluación Inicial)	Determinar el nivel inicial de comprensión conceptual y asegurar la equivalencia de los grupos.
II	2 y 3	Tratamiento Tradicional: Resolución de ejercicios y problemas de cónicas con apoyo del docente.	Tratamiento Experimental: Actividades guiadas y exploratorias de cónicas con GeoGebra.	Implementar el tratamiento experimental para evaluar su influencia en la comprensión conceptual.
III	4	Post-test (Evaluación Final)	Post-test (Evaluación Final)	Determinar la ganancia en la comprensión conceptual de las cónicas en ambos grupos y comparar el efecto de la intervención.

Para el análisis de los datos se utilizaron técnicas estadísticas descriptivas e inferenciales mediante el software SPSS (Pilamunga et al., 2024). Se calcularon medias, desviaciones estándar y diferencias porcentuales entre el pretest y el postest. Asimismo, se aplicó una prueba t de Student para muestras independientes con el fin de determinar si existieron diferencias significativas entre el grupo experimental y el grupo control después del tratamiento  (Castañeda et al., 2010).

RESULTADOS

Los resultados del estudio evidencian diferencias significativas entre los estudiantes del grupo control y el grupo experimental tras la intervención con software de geometría dinámica, en la fase inicial, ambos grupos presentaron niveles comparables de comprensión conceptual sobre las cónicas, con promedios de desempeño ubicados dentro de un rango similar, esta homogeneidad inicial permitió establecer condiciones adecuadas para evaluar el efecto real de la herramienta tecnológica utilizada en el proceso de enseñanza-aprendizaje.

En el pretest, el grupo control obtuvo un puntaje promedio de desempeño ligeramente inferior al del grupo experimental; sin embargo, las desviaciones estándar indican una variabilidad semejante en ambos casos, esto sugiere que la distribución de habilidades matemáticas relacionadas con las cónicas era relativamente uniforme entre los participantes, los análisis preliminares confirman así que no existían diferencias significativas antes de la intervención, lo cual respalda la validez interna del estudio.

Tabla 2: Medias y desviaciones estándar de los puntajes de Pretest y Postest

Grupo	Pretest (Media)	Pretest (DE)	Postest (Media)	Postest (DE)
Control	55.10	7.05	59.18	6.61
Experimental	56.03	7.12	70.03	6.92

Tras la implementación del software de geometría dinámica, los puntajes del grupo experimental mostraron un incremento notable respecto a los resultados obtenidos en el pretest, la diferencia entre pretest y postest en este grupo fue más pronunciada que en el grupo control, donde la mejora fue moderada y asociada principalmente a la instrucción tradicional.

Estos hallazgos sugieren que el uso del software contribuyó sustancialmente al desarrollo de una comprensión conceptual más profunda, el análisis de las medias postest revela que el grupo experimental alcanzó puntajes promedio considerablemente superiores, superando al grupo control por más de diez puntos.

Este aumento fue acompañado de una disminución en la dispersión de los puntajes, lo que indica un aprendizaje más consistente entre los estudiantes que utilizaron el software, en contraste, la variabilidad en el grupo control se mantuvo relativamente alta, lo que sugiere progresos menos homogéneos.

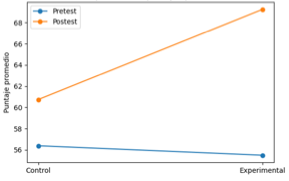
Fig. 1: Comparación de puntajes promedio

En cuanto a la visualización de los datos, los gráficos generados permiten apreciar de manera clara las tendencias identificadas, el gráfico comparativo de medias muestra una separación marcada entre los puntajes postest de ambos grupos, reflejando el efecto positivo de la intervención, por otra parte, el diagrama de caja evidencia una contracción en la dispersión del grupo experimental, indicativa de una apropiación más uniforme del contenido académico.

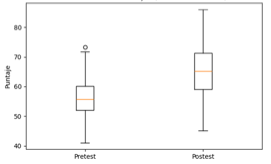
Fig. 2: Distribución de puntajes (pretest vs. postest)

La comparación entre distribuciones refuerza la idea de que el software de geometría dinámica no sólo elevó el nivel general de rendimiento, sino que también consolidó la comprensión conceptual en un mayor número de estudiantes, este patrón sugiere que la herramienta facilitó la manipulación visual y la exploración intuitiva de las propiedades de las cónicas, elementos frecuentemente difíciles de internalizar mediante métodos expositivos tradicionales.

La interpretación global de los resultados permite concluir que la integración de recursos tecnológicos interactivos en el aprendizaje matemático tiene un efecto positivo y significativo en la comprensión conceptual de las cónicas, las mejoras demostradas por el grupo experimental evidencian el potencial pedagógico del software de geometría dinámica para transformar los procesos educativos y favorecer el aprendizaje significativo en estudiantes de bachillerato.

DISCUSIÓN

Los resultados obtenidos en este estudio confirman que el uso de software de geometría dinámica constituye una herramienta eficaz para mejorar la comprensión conceptual de las cónicas en estudiantes de bachillerato, la diferencia significativa entre los puntajes del grupo experimental y el grupo control en el postest respalda la hipótesis de que los entornos interactivos favorecen un aprendizaje más profundo y significativo; este hallazgo coincide con lo que manifiesta Montaño et al. (2023) que destacan el valor de la visualización dinámica para internalizar conceptos matemáticos abstractos.

Una interpretación relevante de estos resultados es que la interacción manipulativa con los objetos geométricos permite que los estudiantes desarrollen modelos mentales más sólidos, a diferencia de la enseñanza tradicional, donde las cónicas se suelen presentar mediante fórmulas y gráficos estáticos, el software permite explorar transformaciones, cambios de parámetros y relaciones entre ecuaciones y representaciones gráficas (Cedeño-Alcívar & Rivadeneira-Loor, 2023).

La mayor homogeneidad en el desempeño del grupo experimental, evidenciada por una reducción en la variabilidad de los puntajes, sugiere que la herramienta tecnológica no solo beneficia a los estudiantes de alto rendimiento, sino que también contribuye a nivelar el aprendizaje entre quienes tradicionalmente presentan dificultades en geometría analítica (Gabriel et al., 2024).

El incremento moderado del grupo control indica que la enseñanza tradicional sigue siendo capaz de generar aprendizaje significativo en cierta medida, especialmente cuando se emplean estrategias pedagógicas claras y estructuradas, sin embargo, la diferencia sustancial entre ambos grupos evidencia que los métodos convencionales no alcanzan el mismo nivel de efectividad cuando se requiere visualizar relaciones geométricas complejas (Solorzano-Marín & Rodríguez-Cedeño, 2023).

Un elemento importante para considerar es que el uso de software de geometría dinámica no solo transforma la forma en la que los estudiantes comprenden las cónicas, sino también el rol del docente en la mediación del conocimiento, durante la intervención, los estudiantes asumieron un papel más activo, exploratorio e investigativo, mientras que el docente facilitó la reflexión y la interpretación (Zambrano-Vera & Rodríguez-Cedeño, 2023).

Los resultados también invitan a reflexionar sobre el potencial motivacional del software interactivo, si bien el estudio se enfocó en la comprensión conceptual y no en variables afectivas, las observaciones durante la intervención sugieren que los estudiantes mostraron mayor interés y participación al utilizar la herramienta, es posible que este incremento en la motivación haya contribuido indirectamente al aprendizaje obtenido, lo cual abre la puerta a futuras investigaciones centradas en componentes socioemocionales del proceso educativo (Pantoja et al., 2024).

A pesar de los resultados positivos, es necesario reconocer algunas limitaciones del estudio, en primer lugar, el tamaño de la muestra, aunque adecuado para análisis descriptivos y comparativos básicos, limita la generalización de los hallazgos a poblaciones más amplias; en segundo lugar, la intervención se aplicó en un periodo relativamente corto, lo que impide evaluar la retención del aprendizaje a largo plazo (Sacón et al., 2025)

La evidencia presentada sugiere que el software de geometría dinámica constituye una herramienta pedagógica valiosa para fortalecer la comprensión conceptual de las cónicas en estudiantes de bachillerato, su capacidad para representar visualmente las interacciones entre ecuaciones y geometría potencia los procesos cognitivos asociados al aprendizaje significativo.

CONCLUSIÓN

Los resultados del estudio permiten concluir que el uso de software de geometría dinámica tiene un impacto significativamente positivo en la comprensión conceptual de las cónicas en estudiantes de bachillerato, la mejora sustancial observada en el grupo experimental, en comparación con el grupo control, evidencia que la interacción con representaciones visuales y manipulables favorece la construcción de significados matemáticos sólidos, esto confirma que las tecnologías dinámicas constituyen un recurso valioso para potenciar el aprendizaje en temas tradicionalmente abstractos y de alta complejidad cognitiva.

Los hallazgos indican que el software no solo mejora el rendimiento promedio, sino que también contribuye a lograr aprendizajes homogéneos entre los estudiantes, reduciendo la dispersión de los puntajes, este resultado sugiere que la herramienta es inclusiva y efectiva incluso para alumnos con dificultades previas en geometría analítica, lo cual representa una ventaja pedagógica relevante, la capacidad del software para vincular ecuaciones, parámetros y representaciones gráficas de manera simultánea genera un entorno interactivo que estimula la exploración y promueve un aprendizaje activo y significativo.

REFERENCIAS

Andrés Sacón Klinger, H., Técnica Luis Vargas Torres Esmeraldas -Ecuador Leidy Virginia Realpe Cancio, U., Técnica Luis Vargas Torres Esmeraldas -Ecuador Sandra Ivett Reasco Angulo, U., Técnica Luis Vargas Torres Esmeraldas -Ecuador Diego Patricio Rosero Bonilla, U., Técnica Luis Vargas Torres Esmeraldas -Ecuador David Saavedra Fuentes, U., Técnica Luis Vargas Torres Esmeraldas -Ecuador José Luis Rodríguez Pullas, U., & Técnica Luis Vargas Torres Esmeraldas -Ecuador, U. (2025). Problemas y Tareas Matemáticas mediante la Aplicación GeoGebra en Educación Superior: Problems and Mathematical Tasks Using the GeoGebra Application in Higher Education. LATAM Revista Latinoamericana de Ciencias Sociales y Humanidades, 6(1), 2536-2543–2536 – 2543. https://doi.org/10.56712/LATAM.V6I1.3514

Barallobres, G., & Barallobres, G. (2016). Diferentes interpretaciones de las dificultades de aprendizaje en matemática. Educación Matemática, 28(1), 39–68. https://doi.org/10.24844/EM2801.02

Bozzano, H. R., Frediani, J. C., Cirio, G. W., & Barrionuevo, C. A. (2020). Metodología de la investigación en Geografía. Metodología de La Investigación En Geografía. https://doi.org/10.35537/10915/57355

Castañeda, M. B., Cabrera, A., Navarro, Y., & De Vries, W. (2010). Procesamiento de datos y análisis estadísticos utilizando SPSS (1st ed., Vol. 1). EDIPUCRS. https://www.researchgate.net/profile/Alberto-Cabrera/publication/261704346_Procesamiento_de_datos_y_analisis_estadisticos_utilizando_SPSS_Un_libro_practico_para_investigadores_y_administradores_educativos/links/00b4953510e4a0dd01000000/Procesamiento-de-datos-y-analisis-estadisticos-utilizando-SPSS-Un-libro-practico-para-investigadores-y-administradores-educativos.pdf

Cedeño-Alcívar, J. C., & Rivadeneira-Loor, F. Y. (2023). GeoGebra como Herramienta Didáctica para la Enseñanza de la Matemática. MQRInvestigar , 7(4), 634–649. https://doi.org/10.56048/MQR20225.7.4.2023.634-649

Enrique, W., & Fernandez, P. (2020). Resolución de problemas matemáticos en GeoGebra. Revista Do Instituto GeoGebra Internacional de São Paulo, 9(1), 26–42. https://doi.org/10.23925/2237-9657.2020.V9I1P26-42

Estrategia Didáctica El Proceso De Enseñanza Aprendizaje De La Matemática, C. E., Rubén de León Rodríguez, N., Alexander Santy Ruales, W., Augusto Ortiz Palacios, C., Maribel Paredes Proaño, A., & Paquita Camacho Cañar, E. (2022). La evaluación diagnóstica como estrategia didáctica en el proceso de enseñanza aprendizaje de la Matemática. Universidad y Sociedad, 14(S5), 583-594. https://rus.ucf.edu.cu/index.php/rus/article/view/3327

Gabriel, J., Guevara, B., General, U. E., Andrade Bolívar -Ecuador, J., Camila, A., & Revelo, C. (2024). GeoGebra y el rendimiento académico en el aprendizaje de funciones reales: GeoGebra and academic performance in learning real-world functions. LATAM Revista Latinoamericana de Ciencias Sociales y Humanidades, 5(6), 1767-1777–1767 – 1777. https://doi.org/10.56712/LATAM.V5I6.3121

KOINONIA Santa Ana de Coro Venezuela Juana Giselle Burgos-Macías, F., Giselle Burgos-Macías, J., Cesar Vallejo Piura, U., & Perú, P. (2024). Aprendizaje significativo matemático basado en la educación emocional. Revista Arbitrada Interdisciplinaria Koinonía, 9(17), 257–275. https://doi.org/10.35381/r.k.v9i17.3218

López, S. M., & Noguera, S. G. (2026). What is GeoGebra Discovery? An illustration: ¿Qué es GeoGebra Discovery? Una ilustración. Revista Digital: Matemática, Educación e Internet, 26(1). https://doi.org/10.18845/RDMEI.V26I1.7981

Montaño, D. P., Superior, I., Loja, T., Osler, L.-E., & Marín, Q. V. (2023). Uso de GeoGebra para generar aprendizajes significativos de las secciones cónicas: Use of GeoGebra to generate meaningful learning of conic sections. LATAM Revista Latinoamericana de Ciencias Sociales y Humanidades, 4(5), 65-85–65–85. https://doi.org/10.56712/LATAM.V4I5.1302

Palacios-Hidalgo, F. J., & Cimas, J. G. (2024). Percepciones del profesorado de matemáticas sobre la gamificación: Conocimiento, formación y utilidad. Bolema: Boletim de Educação Matemática, 38, e230080. https://doi.org/10.1590/1980-4415V38A230080

Pantoja Chávez, D. G., Trujillo Ruiz, E. L., Anahi Iveth, I. B., Zambrano Chávez, A. A., & Zambrano Chávez, J. E. (2024). Efectividad de la Evaluación Formativa y Sumativa en el Aprendizaje Profundo y la Retención a Largo Plazo. Ciencia Latina Revista Científica Multidisciplinar, 8(5), 13368–13383. https://doi.org/10.37811/CL_RCM.V8I5.14791

Pilamunga, C., Orlando, B., Educativa, U., Flor, F., López, C., Bernave, M., Monar, G., Rocío, K., Sarango, H., Fernando, A., Superior, I., & España, T. (2024). Chi Cuadrado y tablas de contingencia aplicado en SPSS. Código Científico Revista de Investigación, 5(E3), 499–513. https://doi.org/10.55813/GAEA/CCRI/V5/NE3/329

Romero, M. Á. M., & Alvarado, R. A. R. (2025). Metodología, difusión y divulgación de la investigación científica. Guía estratégica para producir y comunicar conocimiento. Religacion Press. https://doi.org/10.46652/RELIGACIONPRESS.314

Rubio-Pizzorno, S., & Espinosa, G. M. (2021). Socially constructed Virtual Learning Environments with GeoGebra Authoring Tools. Innovaciones Educativas, 23(34), 213–227. https://doi.org/10.22458/IE.V23I34.3432

Solorzano-Marín, J. O., & Rodríguez-Cedeño, F. V. (2023). GeoGebra como herramienta interactiva en la resolución de problemas de función cuadrática. MQRInvestigar , 7(4), 1706–1720. https://doi.org/10.56048/MQR20225.7.4.2023.1706-1720

Zambrano-Vera, M. L., & Rodríguez-Cedeño, F. V. (2023). GeoGebra como estrategia didáctica en la enseñanza de matrices. MQRInvestigar , 7(3), 2752–2767. https://doi.org/10.56048/MQR20225.7.3.2023.2752-2767