Estrategias lúdicas de retroalimentación mediante pausas activas para fortalecer las multiplicaciones en estudiantes de educación básica
Playful feedback strategies using active pauses to strengthen multiplication in elementary school students
Sandra María Anzo Ortega1 y Edgar Escobar Gutierrez2
1Universidad Contemporánea de las Américas, s_anzo@inaesdi.com, https://orcid.org 0009-0003-5897-6495, México
2Universidad Contemporánea de las Américas, edgar.e.g@unicla.edu.mx, https://orcid.org/0009-0002-4237-6092, México
|
Información del Artículo |
|
RESUMEN |
|
|
Trazabilidad: Recibido 27-03-2025 Revisado 28-03-2025 Aceptado 12-04-2025
|
|
Este estudio se centra en las dificultades que enfrentan los estudiantes de educación básica en la comprensión de la multiplicación y el papel que las estrategias lúdicas pueden desempeñar en su aprendizaje. Se argumenta que una sólida comprensión de las operaciones matemáticas es esencial para el éxito académico y el desarrollo de habilidades necesarias para la vida cotidiana. La investigación implementa un enfoque cuantitativo, utilizando una encuesta estructurada y una muestra de 37 alumnos para recoger datos sobre sus percepciones y actitudes hacia el aprendizaje matemático. Los hallazgos indican que existe una relación significativa entre el uso de actividades lúdicas y la mejora en el aprendizaje de la multiplicación, evidenciando que la motivación y la comprensión se benefician de métodos didácticos activos. Además, se identifican desafíos contextuales, como los efectos de la pandemia y los cambios en los planes de estudio, que afectan el desarrollo académico. La investigación concluye que las estrategias lúdicas no solo fomentan un ambiente de aprendizaje positivo, sino que también son efectivas para fortalecer la capacidad de los estudiantes para resolver problemas matemáticos. Se sugiere que futuros estudios deben explorar metodologías diversas, ampliar las muestras a diferentes contextos y evaluar resultados a largo plazo para enriquecer la enseñanza de las matemáticas. |
|
|
Palabras Clave: Estrategias lúdicas Aprendizaje Multiplicación |
|||
|
|
|||
|
Keywords: Playful strategies Learning Multiplication |
|
ABSTRACT This study focuses on the difficulties faced by elementary school students in understanding multiplication and the role that playful strategies can play in their learning. It argues that a solid understanding of mathematical operations is essential for academic success and the development of skills necessary for everyday life. The research implements a quantitative approach, using a structured survey and a sample of 37 students to collect data on their perceptions and attitudes toward mathematics learning. The findings indicate a significant relationship between the use of playful activities and improved multiplication learning, demonstrating that motivation and understanding benefit from active teaching methods. Furthermore, contextual challenges, such as the effects of the pandemic and curriculum changes, are identified as affecting academic development. The research concludes that playful strategies not only foster a positive learning environment but are also effective in strengthening students' ability to solve mathematical problems. It is suggested that future studies should explore diverse methodologies, expand samples to different contexts, and evaluate long-term outcomes to enrich mathematics teaching.
|
||
|
||||
INTRODUCCIÓN
El presente estudio se centra en las dificultades que enfrentan los estudiantes de educación básica en la comprensión de la multiplicación, como hace referencia (Gil Rubio, 2016) “Las matemáticas no son una ciencia de memorización, si no de comprensión” ya que es un aspecto fundamental del aprendizaje matemático. La comprensión sólida de las operaciones básicas, como la multiplicación, es crucial no solo para el éxito académico en matemáticas, sino también para el desarrollo de habilidades esenciales que los estudiantes necesitarán en niveles educativos superiores y en su vida cotidiana, afirma (Universidad Espiritu Santo, 2022) “Las matemáticas son una herramienta muy importante para la vida, pues son la clave del éxito en todos los campos y nos rodean por todas partes”. La falta de competencia en esta área puede limitar la capacidad de los alumnos para abordar temas más complejos y solucionar problemas matemáticos en contextos más avanzados, lo que repercute negativamente en su rendimiento académico general.
Diversas investigaciones han evidenciado que el aprendizaje significativo se logra cuando los estudiantes pueden conectar los conceptos teóricos con situaciones prácticas. Como menciona (Contreras, 2016) en su artículo El aprendizaje significativo y su relación con otras estrategias, “El aprendizaje y retención de carácter significativo, basados en la recepción, son importantes en la educación porque son los mecanismos humanos “par excellence” para adquirir y almacenar la inmensa cantidad de ideas e información que constituye cualquier campo de conocimiento” En este contexto, las estrategias lúdicas, tienen el potencial de transformar la enseñanza de la multiplicación. La integración de actividades recreativas y juegos matemáticos en el aula no solo promueve la motivación, sino que también enriquece la participación activa de los estudiantes en el proceso de aprendizaje. Esta metodología se basa en la premisa de que aprender matemáticas puede y debe ser una experiencia divertida y estimulante, que fomente el pensamiento crítico y fortalezca la comprensión de los conceptos.
La problemática en cuestión se ve agravada por factores contextuales, como los efectos de la pandemia por COVID-19, que llevaron a una interrupción prolongada del aprendizaje presencial. Como postula (Programa de las Naciones Unidas Para el Desarrollo, 2022) “Es de esperar que el cierre de las escuelas ocasionado por la pandemia de la COVID-19, así como el abandono y truncamiento asociados, tenga repercusiones de largo plazo en los alumnos”, lo cual causó que muchos estudiantes no lograran consolidar adecuadamente sus conocimientos previos, particularmente en áreas fundamentales como la multiplicación. Al mismo tiempo, los cambios en los planes de estudio, desde "Aprendizajes Clave 2017" a los nuevos "Programas de Estudio 2022" de la Nueva Escuela Mexicana, han introducido desafíos adicionales al permitir que los docentes decidan cómo abordar los contenidos en el aula. Esta flexibilidad, aunque potencialmente beneficiosa, también puede resultar en una falta de profundidad en la enseñanza de conceptos clave, creando un vacío en el desarrollo académico que afectará a los estudiantes a largo plazo. Para abordar esta situación, las preguntas de investigación se diseñan para explorar tanto las dificultades específicas que enfrentan los estudiantes como los métodos que podrían ayudar a superarlas. Estas preguntas no solo permitirán profundizar en el diagnóstico de los problemas existentes, sino que también buscarán identificar estrategias efectivas que contribuyan a la enseñanza de la multiplicación. Entre ellas, se indaga sobre el impacto que podrían tener las pausas activas en el aprendizaje lúdico y cómo estas podrían influir positivamente en la motivación y en la capacidad de los alumnos para resolver problemas matemáticos.
La hipótesis del estudio sostiene que habrá una relación significativa entre la implementación de estrategias lúdicas y la mejora en el aprendizaje de la multiplicación. Esta hipótesis se formulará en términos de una declaración nula, que propone que no existe tal relación, y servirá como un punto de partida para contrastar la hipótesis de investigación mediante análisis estadísticos. La confirmación o refutación de esta hipótesis permitirá no solo validar la efectividad de la estrategia propuesta, sino también contribuir al desarrollo de un modelo educativo que integre el juego como herramienta pedagógica en la enseñanza de las matemáticas. Como afirma (Yalda, 2017) “Las hipótesis indican lo que tratamos de probar y se definen como explicaciones tentativas del fenómeno investigado”.
Este marco de investigación tiene como finalidad abordar de manera integral las dificultades actuales en la comprensión de la multiplicación entre los estudiantes de educación básica. A través de una combinación de estrategias lúdicas, análisis críticos y un enfoque en las necesidades específicas del contexto educativo contemporáneo, se busca proporcionar una solución que fomente un aprendizaje significativo y sostenible en las matemáticas, preparando así a los estudiantes para enfrentar los retos académicos futuros.
MATERIALES Y MÉTODOS
Para la presente investigación se seleccionó como herramienta de recolección de datos una encuesta estructurada, debido a su eficacia para obtener información directa de los participantes de manera rápida y sistemática. Este instrumento fue diseñado con el objetivo de recopilar datos relevantes que permitieran analizar la relación entre las variables establecidas en el estudio. El cuestionario estuvo conformado por un total de 9 ítems cuidadosamente elaborados, orientados a indagar aspectos específicos relacionados con los objetivos de la investigación. Cada pregunta fue diseñada para captar las percepciones, actitudes o comportamientos de los encuestados respecto al fenómeno en estudio.
Para la medición de las respuestas se utilizó una escala de Likert de cinco puntos, una de las técnicas más utilizadas en investigaciones de tipo cuantitativo. Esta escala ofrece un rango de opciones que va desde "Totalmente en desacuerdo", "En desacuerdo", "Ni de acuerdo ni en desacuerdo", "De acuerdo" hasta "Totalmente de acuerdo". Su uso permite transformar percepciones cualitativas en datos cuantificables, facilitando así el análisis estadístico posterior. La elección de esta escala respondió a la necesidad de capturar con mayor precisión el grado de conformidad o desacuerdo de los participantes frente a cada afirmación planteada. Asimismo, contribuye a medir de forma más fiable y objetiva las actitudes o creencias de los sujetos frente a las variables analizadas.
El tipo de muestreo para la investigación es probabilístico ya que (Otzen, 2017) define que “Las técnicas de muestreo probabilísticas, permiten conocer la probabilidad que cada individuo a estudio tiene de ser incluido en la muestra a través de una selección al azar.” La muestra para esta investigación está conformada por 37 alumnos de educación básica, seleccionados de una población total de 41 estudiantes. Esta cantidad se determinó considerando un nivel de confianza del 95% y un margen de error del 5%. El resultado se obtuvo mediante la aplicación de la fórmula para el cálculo de muestras en poblaciones finitas, la cual se presenta en la Tabla 1:
Tabla 1: Muestra
|
n= |
37 |
|
nivel de confianza |
95.00% |
|
valor de Z |
1.96 |
|
p= |
50.00% |
|
q= |
50.00% |
|
e= |
5.00% |
|
N= |
41.00 |
Una vez determinado el total de alumnos que conforman la muestra de estudio, se procede a comprobar la fiabilidad del instrumento de recolección de datos mediante el coeficiente Alpha de Cronbach. El resultado de este análisis se presenta en la Tabla 2:
Tabla 2: Fiabilidad
|
Estadísticas de fiabilidad |
|
|
Alfa de Cronbach |
N de elementos |
|
.814 |
9 |
Según los criterios generalmente aceptados en la literatura metodológica, un valor de Alpha de Cronbach se interpreta de la siguiente manera:
- ≥ 0.90: Excelente
- 0.80 – 0.89: Buena
- 0.70 – 0.79: Aceptable
- 0.60 – 0.69: Cuestionable
- < 0.60: Baja o inaceptable
Dado que el valor obtenido es 0.814, se concluye que el instrumento presenta una fiabilidad buena, lo que indica que los ítems incluidos están adecuadamente relacionados entre sí y miden de manera consistente el constructo objeto de estudio.
Una vez obtenidos resultados favorables tanto en la determinación de la muestra como en la fiabilidad del instrumento, se procede a la elección del paradigma, enfoque, tipo de investigación y método, con el objetivo de establecer un contraste metodológico riguroso de los resultados. El paradigma seleccionado es el constructivista, ya que parte del principio de que, a partir de la información recopilada mediante instrumentos adecuados, es posible construir conocimiento. Este paradigma brinda la base para adoptar un enfoque cuantitativo, dado que los datos obtenidos a través de los instrumentos son de naturaleza numérica. En concordancia con lo anterior, se opta por un tipo de investigación correlacional, ya que permite analizar la relación entre variables. Finalmente, para el contraste de las hipótesis planteadas, se emplea el método hipotético-deductivo, el cual posibilita evaluar supuestos a partir de la evidencia empírica recogida.
.
RESULTADOS Y DISCUSIÓN
Como parte del análisis de resultados, y en concordancia con el tipo de investigación correlacional seleccionado, se decide aplicar una matriz de correlación entre los distintos elementos del instrumento. Esta herramienta permite identificar los coeficientes que presentan mayor relevancia en relación con el fenómeno de estudio. El objetivo de este análisis es determinar qué variables o elementos guardan una asociación significativa, lo cual contribuye a una comprensión más profunda del comportamiento del fenómeno observado. A continuación, se presenta la matriz de correlación obtenida entre los elementos evaluados:
Tabla 3: Relación Entre Elementos
|
Matriz de correlaciones entre elementos |
||||
|
|
Las clases de matemáticas me parecen fáciles de entender. |
Me siento motivado(a) a participar en las actividades matemáticas. |
Aprendo mejor cuando las clases incluyen juegos o actividades lúdicas. |
Las actividades creativas (como dibujos, juegos o dinámicas) me ayudan a comprender mejor las matemáticas. |
|
Las clases de matemáticas me parecen fáciles de entender. |
1.000 |
0.156 |
0.098 |
-0.042 |
|
Me siento motivado(a) a participar en las actividades matemáticas. |
0.156 |
1.000 |
0.605 |
0.515 |
|
Aprendo mejor cuando las clases incluyen juegos o actividades lúdicas. |
0.098 |
0.605 |
1.000 |
0.445 |
|
Las actividades creativas (como dibujos, juegos o dinámicas) me ayudan a comprender mejor las matemáticas. |
-0.042 |
0.515 |
0.445 |
1.000 |
Como se puede observar en la Tabla 3, se presentan tanto coeficientes de correlación positivos como negativos, los cuales serán analizados con el propósito de interpretar los resultados en función del fenómeno de estudio. Estos coeficientes permiten identificar la dirección y la fuerza de las relaciones entre los elementos evaluados, lo que aporta información valiosa para comprender cómo interactúan las variables dentro del contexto investigado. La matriz presentada refleja las correlaciones entre distintos enunciados relacionados con la experiencia de los estudiantes en las clases de matemáticas. El análisis se centra en la dirección (positiva o negativa) y la fuerza de las relaciones entre los elementos, utilizando el coeficiente de correlación de Pearson (r), cuyo rango va de -1 a 1.
Relaciones clave entre los elementos:
- Relación entre "Me siento motivado(a) a participar en las actividades matemáticas" y "Aprendo mejor cuando las clases incluyen juegos o actividades lúdicas" (r = 0.605):
- Se observa una correlación positiva moderada-alta, lo que indica que quienes se sienten motivados también tienden a aprender mejor cuando las clases incluyen actividades lúdicas. Esto sugiere que la motivación y los métodos activos de enseñanza están estrechamente relacionados.
- Relación entre "Las clases de matemáticas me parecen fáciles de entender" y los demás elementos:
- Con "actividades creativas" (r = -0.042), se observa una correlación negativa muy baja, prácticamente inexistente. Esto indica que la percepción de facilidad en la materia no está relacionada con el uso de actividades creativas en este grupo.
La matriz revela que los elementos relacionados con la motivación y el uso de recursos lúdicos y creativos muestran correlaciones positivas significativas entre sí, lo que sugiere que implementar métodos didácticos activos puede tener un impacto favorable en la motivación y comprensión de las matemáticas. Por otro lado, la percepción de facilidad en las clases parece estar menos relacionada con estas estrategias, lo cual puede indicar que la comprensión y la motivación responden a factores distintos.
Con base en los resultados obtenidos previamente, se procede a la interpretación de los datos a través del análisis de correlaciones de frecuencias. Este proceso permite identificar la fuerza y dirección de las relaciones entre los distintos elementos evaluados, lo que facilita una comprensión más profunda del fenómeno de estudio. A continuación, se presentan los resultados derivados de este análisis en la ilustración 1:
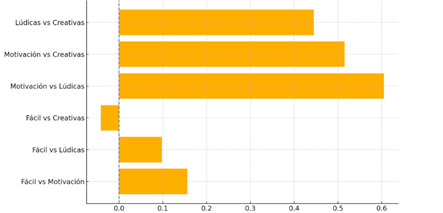
Fig. 1: Frecuencias de correlaciones
El gráfico muestra la fuerza y dirección de la relación entre diferentes elementos relacionados con el aprendizaje de matemáticas, según los coeficientes de correlación:
- Las correlaciones más altas se observan entre:
- "Motivación vs Lúdicas" (0.605): indica que los estudiantes motivados tienden a aprender mejor cuando hay actividades lúdicas.
- Correlaciones bajas o débiles:
- "Fácil vs Creativas" (-0.042): una correlación negativa muy leve, lo que sugiere que percibir la clase como fácil no depende del uso de recursos creativos.
El gráfico evidencia que los métodos didácticos activos (juegos, dinámicas, creatividad) están fuertemente relacionados con la motivación y la comprensión, más que con la simple percepción de facilidad. Esto destaca la importancia de estrategias pedagógicas innovadoras en la enseñanza de matemáticas. La hipótesis planteada en esta investigación establece que "habrá una relación significativa entre la implementación de estrategias lúdicas y la mejora en el aprendizaje de la multiplicación". A partir del análisis de correlaciones, se observaron relaciones positivas moderadas a altas entre los siguientes elementos:
- La motivación de los estudiantes y el uso de actividades lúdicas (r = 0.605),
Estos resultados respaldan la hipótesis, ya que indican que la aplicación de estrategias lúdicas está asociada con una mayor motivación y una mejor comprensión de los contenidos matemáticos, lo cual repercute directamente en el aprendizaje de la multiplicación. Por tanto, se concluye que sí existe una relación significativa entre la implementación de estrategias lúdicas y la mejora del aprendizaje de la multiplicación en los estudiantes, validando empíricamente la hipótesis de investigación.
CONCLUSIÓN
A partir de toda la información recopilada, así como del análisis e interpretación de los resultados obtenidos, es posible establecer las siguientes conclusiones y recomendaciones, las cuales permiten dar cierre al presente estudio y ofrecer aportes significativos para futuras intervenciones educativas.
- Relación significativa entre estrategias lúdicas y aprendizaje: Los resultados obtenidos respaldan la hipótesis de que existe una relación significativa entre la implementación de estrategias lúdicas y la mejora en el aprendizaje de la multiplicación entre los estudiantes de educación básica. Los datos muestran que los estudiantes motivados tienden a aprender mejor cuando se utilizan actividades lúdicas, lo que resalta la importancia de estas estrategias en el proceso educativo.
- Impacto positivo en la motivación y comprensión: La investigación evidencia que el uso de métodos didácticos activos, como juegos y actividades recreativas, no solo fomenta la motivación de los alumnos, sino que también mejora su comprensión de los conceptos matemáticos. Esto sugiere que los enfoques innovadores en la enseñanza son clave para abordar las dificultades en aprendizaje matemático.
- Desafíos contextuales y oportunidades de mejora: A pesar de los beneficios de las estrategias lúdicas, la investigación también identifica desafíos contextuales que afectan el aprendizaje, como el impacto de la pandemia. Se destaca la necesidad de un enfoque integral que considere tanto las dinámicas del aula como las influencias externas en la educación de los estudiantes.
AGRADECIMIENTOS
Con gran satisfacción y gratitud, expreso mi más sincero agradecimiento por haber culminado satisfactoriamente esta investigación, la cual representa un paso significativo en mi formación profesional.
De manera especial, agradezco a la Universidad Contemporánea de las Américas por brindarnos no solo el espacio académico, sino también las herramientas necesarias para llevar a cabo este proyecto y, sobre todo, por permitirnos adquirir conocimientos que podremos aplicar en nuestro ámbito laboral, contribuyendo así al desarrollo educativo de nuestra comunidad.
Asimismo, extiendo mi profundo agradecimiento al Dr. Edgar Escobar Gutiérrez, mi asesor de investigación, por su tiempo, dedicación y guía constante a lo largo de este proceso. Su acompañamiento y experiencia fueron fundamentales para alcanzar los objetivos planteados.
A todos los que formaron parte de este camino, gracias por su apoyo incondicional.
REFERENCIAS
Contreras, F. (2016). El aprendizaje significativo y su relación con otras estrategias. Horizonte de la ciencia, 6(10), 130-140. https://doi.org/https://doi.org/10.26490/uncp.horizonteciencia.2016.10.210
Gil Rubio, C. (2016). https://zaguan.unizar.es/. https://zaguan.unizar.es/: https://zaguan.unizar.es/record/48469/files/TAZ-TFG-2016-215.pdf
Otzen, S. (2017). Técnicas de Muestreo sobre una Población a Estudio. International Journal of Morphology, 35, 227-232. https://doi.org/http://dx.doi.org/10.4067/S0717-95022017000100037
Programa de las Naciones Unidas Para el Desarrollo. (2022). https://www.undp.org/. https://www.undp.org/: https://www.undp.org/sites/g/files/zskgke326/files/2022-07/COVID19%20y%20educaci%C3%B3n%20en%20M%C3%A9xico.pd
Universidad Espiritu Santo. (15 de Febrero de 2022). https://uees.edu.ec/. https://uees.edu.ec/: https://uees.edu.ec/las-matematicas-en-la-vida-cotidiana/
Yalda, L. (2017). https://pediatrianorte.med.uchile.cl/. https://pediatrianorte.med.uchile.cl/: https://pediatrianorte.med.uchile.cl/investigacion/cursos/Hipotesis%20y%20objetivos.pdf