Modelación matemática en la comprensión conceptual y la habilidad de resolver problemas en estudiantes de Ciencias Administrativas y Económicas
Mathematical modeling in the conceptual understanding and problem-solving skills of students of Administrative and Economic Sciences
Johnny Mauricio Lima Narváez1, Carlos Jeovanny Villegas López2, Mónica Esther Clerque Cevallos3, Elizabeth Vanesa Chaluiza Charro4 y Elsa Rocío Arequipa Quishpe5
1Universidad Técnica del Norte, jmlima@utn.edu.ec, https://orcid.org/0000-0001-7248-2211, Ecuador
2Ministerio de Educación, carlos.villegas@educacion.gob.ec, https://orcid.org/0009-0009-2941-055X, Ecuador
3Ministerio de Educación, monica.clerque@educacion.gob.ec, https://orcid.org/0009-0006-0688-2958, Ecuador
4Universidad Central del Ecuador, evchaluiza@uce.edu.ec, https://orcid.org/0009-0007-1121-4126, Ecuador
5Universidad Central del Ecuador, earequipa@uce.edu.ec, https://orcid.org/0000-0002-1238-8220, Ecuador
|
Información del Artículo |
|
RESUMEN |
|
|
Trazabilidad: Recibido 02-10-2025 Revisado 03-10-2025 Aceptado 05-11-2025
|
|
Esta investigación analizó la estructura, el rendimiento y la relación entre las competencias Modelación Matemática, Comprensión Conceptual y la Habilidad para Resolver Problemas en una muestra de 119 estudiantes de en el campo de las Ciencias Administrativas y Económicas. El problema principal fue establecer el grado de dominio de estas capacidades y su dependencia con la carrera estudiada. Los análisis descriptivos mostraron un rendimiento general moderado, donde la habilidad de resolver problemas era el área más frágil y variada. La prueba de Kolmogorov-Smirnov mostró que no hay una distribución normal, lo que valida el empleo de pruebas no paramétricas. Los resultados más importantes indican una dependencia evidente del rendimiento por carrera: aunque la carrera de Administración de Empresas tuvo el mejor desempeño, Contabilidad y Auditoría evidenció una debilidad notable en cuanto a la Habilidad para Resolver Problemas. La Modelación Matemática y la Comprensión Conceptual están fuertemente relacionadas, según el análisis de correlación de Spearman, que mostró una sólida validez estructural entre las competencias. Sin embargo, el hecho de que la habilidad de resolver problemas tenga la correlación más baja con las otras variables indica que es el componente más autónomo del constructo. Se llega a la conclusión de que las intervenciones curriculares deben concentrarse en el desarrollo de la aplicación práctica, dando prioridad a una perspectiva diferenciada y centrada en la carrera de Auditoría y Contabilidad. |
|
|
Palabras Clave: Modelación Matemática Comprensión Conceptual Habilidad de Resolver Problemas |
|||
|
|
|||
|
Keywords: Mathematical Modeling Conceptual Understanding Problem-Solving Skills |
|
ABSTRACT This research analyzed the structure, performance, and relationship between the competencies of Mathematical Modeling, Conceptual Understanding, and Problem-Solving Ability in a sample of 119 students in the field of Administrative and Economic Sciences. The main problem was to establish the degree of mastery of these skills and their dependence on the specific program of study. Descriptive analyses showed moderate overall performance, with Problem-Solving Ability being the weakest and most varied area. The Kolmogorov-Smirnov test indicated a lack of normal distribution, thus validating the use of non-parametric tests. The most important findings point to a clear dependence of performance on the degree program: although the Business Administration program exhibited the best performance, Accounting and Auditing showed a notable weakness concerning Problem-Solving Ability. Mathematical Modeling and Conceptual Understanding are strongly related, according to Spearman's correlation analysis, which demonstrated a solid structural validity among the competencies. However, the fact that Problem-Solving Ability has the lowest correlation with the other variables indicates that it is the most autonomous component of the construct. The conclusion is that curricular interventions must focus on the development of practical application, prioritizing a differentiated and targeted approach for the Accounting and Auditing program. |
||
|
||||
INTRODUCCIÓN
La educación superior se enfrenta al reto permanente de ir más allá de la instrucción teórica, lo que requiere que los estudiantes universitarios sean capaces de utilizar conocimientos abstractos para resolver problemas complejos y multifacéticos del mundo real (García & Pérez, 2021). La Modelación Matemática se presenta como una estrategia pedagógica esencial en este contexto, ya que conecta el formalismo de las matemáticas con la fenomenología de varias áreas, desde la ingeniería hasta las ciencias sociales (López et al., 2020). Esta perspectiva se extiende más allá de la simple computación, alentar un ciclo de formulación, solución, interpretación y validación de modelos, capacidades que los expertos del siglo XXI consideran fundamentales (Ramírez & Soto, 2022). Los estudios recientes han resaltado la urgencia de incorporar metodologías activas que promuevan un aprendizaje significativo y transferible (Martínez & Bravo, 2023).
Según investigaciones meta-analíticas recientes, la aplicación de programas de modelación matemática incrementa el tamaño del efecto en las capacidades de pensamiento superior en un 0.65 frente a la enseñanza tradicional, una conclusión que destaca su fuerza pedagógica (Duarte & Cárdenas, 2024). En particular, la investigación sugiere que el desarrollo cognitivo se ve beneficiado con la aplicación estricta de la modelación matemática. Al exigir que los alumnos conviertan situaciones no estructuradas en representaciones matemáticas, se fomenta una comprensión más profunda de los conceptos subyacentes a los fenómenos (Silva et al., 2021). Por otro lado, sigue siendo un problema el escaso rendimiento al aplicar conocimientos. Una investigación a gran escala en universidades técnicas mostró que solo el 35 % de los graduados poseían la capacidad efectiva para modelar y solucionar problemas no rutinarios en el entorno laboral, lo que señala una deficiencia significativa en la capacitación brindada (Morales & Rojas, 2020).
No obstante, la evidencia que mide de manera directa el impacto de la modelación a nivel universitario, sobre todo en términos de cotejo de resultados con técnicas tradicionales, todavía necesita una sólida y actualizada fundamentación empírica (Vega & Castro, 2024). La importancia de este estudio se debe a que los resultados del aprendizaje tienen dos dimensiones. Por un lado, se intenta evaluar el progreso en la comprensión de conceptos, esto es, qué tan bien los alumnos asimilan la teoría subyacente al fenómeno. Por otra parte, se examina la capacidad para resolver problemas, que es una competencia práctica para emplear el modelo como instrumento de predicción o explicación (Fuentes & Herrera, 2023). La modelación está fuertemente correlacionada con el desarrollo de la competencia de pensamiento crítico, según investigaciones anteriores que se han centrado en la educación secundaria (Jiménez & Núñez, 2022).
Por lo tanto, es fundamental cuantificar el impacto directo de esta estrategia a nivel universitario (Pérez & Díaz, 2020), en donde los problemas reales son intrínsecamente más complejos y multidisciplinarios. Este estudio actual trata dicha brecha a través de la evaluación cuantitativa del efecto de la implementación de modelación matemática en el progreso de la capacidad para resolver problemas y la comprensión conceptual en estudiantes de Ciencias Administrativas y Económicas. El propósito principal es establecer si los estudiantes que han sido expuestos a esta metodología logran niveles significativamente más altos en estas variables dependientes comparados con un grupo de control. Los resultados ayudarán a la evidencia científica requerida para sustentar la reforma de los planes de estudio en educación superior, fomentando la modelación matemática no solamente como un contenido, sino también como una pedagogía crucial para capacitar a profesionales con habilidades para enfrentar la incertidumbre y complejidad en su área (Quintero & Rojas, 2024).
MATERIALES Y MÉTODOS
En este estudio, se utilizó como método principal para recopilar datos una encuesta estructurada, creada con el objetivo de adquirir información meticulosa, exacta y sistemática sobre las variables en análisis. Este procedimiento es descrito por varios autores en el ámbito metodológico, incluyendo a Landaluce (2024), como "un proceso de investigación empírica, auto administrado o mediado, que se realiza con una muestra de individuos y emplea un cuestionario estandarizado para recoger sus puntos de vista y valoraciones" (p. 251). Esta encuesta se compone de 18 ítems o reactivos cuidadosamente diseñados, basados en una escala de Likert. Mediante la adopción de la escala Likert, se ofrece un sólido respaldo metodológico, dado que permite cuantificar las actitudes y percepciones de los participantes a través del empleo de alternativas de respuesta graduadas. Esta característica hace que el análisis estadístico de los datos recopilados sea mucho más fácil después. En esta línea, Méndez et al. mencionan que la técnica original de Likert es "un método de escalamiento que se ideó en la investigación social para asignar un valor numérico a las opiniones, el nivel de acuerdo o las actitudes que los individuos expresan frente a una afirmación concreta" (2021, p. 35).
La razón principal para implementar este tipo de instrumento es de dos tipos: en primer lugar, identificar las interrelaciones entre los ítems del cuestionario; en segundo lugar, evaluar su coherencia o consistencia interna. Esta última es una propiedad crucial de la confiabilidad, ya que es clave para el análisis e interpretación de los resultados más adelante, por medio de métodos estadísticos descriptivos e inferenciales. La población de estudio incluye a 119 estudiantes de carreras en Ciencias Administrativas y Económicas, la selección de estos participantes se llevó a cabo utilizando rigurosos criterios de inclusión, con el fin de asegurar la homogeneidad en elementos importantes para el estudio. Estos rasgos incluyen el nivel académico, el ambiente educativo y la experiencia anterior de los estudiantes en el campo de estudio.
La
investigación actual se encuentra en línea con el enfoque positivista, que se
caracteriza por dar prioridad al uso sistemático del método científico como
medio legítimo para producir conocimiento objetivo, comprobable y capaz de ser
generalizado. Valarezo et al.caracterizan el positivismo, en su versión
científica, como "la corriente filosófica que basa el conocimiento
solamente en la experiencia sensible, la observación de los hechos y sus
conexiones, negando cualquier proposición metafísica o apriorística" (2020,
p. 268). Este enfoque metodológico sostiene que, al identificar patrones o
leyes de conexión entre fenómenos, es posible medir, observar y explicar la
realidad. Por lo tanto, se enfoca en recolectar datos que puedan ser
cuantificados para determinar conexiones sólidas entre las variables. De
acuerdo con esta perspectiva epistemológica, se ha tomado un método de tipo
cuantitativo como fundamento de la metodología. Según Hernández-Sampieri y
Mendoza "la investigación cuantitativa utiliza la recopilación y el
análisis de datos para responder preguntas de investigación y comprobar
hipótesis previamente formuladas, basándose en la medición numérica, el conteo
y la estadística" (2020, p. 3). La naturaleza del problema investigado y
la clase de instrumento elegido hacen que esta perspectiva esté plenamente
justificada.
En este contexto, se eligió la encuesta estructurada porque tiene la capacidad
de reunir datos objetivos y numéricos estandarizados. Este instrumento no solo
simplifica la recolección de datos que se pueden comparar, sino que además
mejora el análisis estadístico posterior, lo cual es un requisito indispensable
para alcanzar los objetivos de la investigación planteados. La investigación
utilizará un diseño correlacional porque su principal propósito es analizar el
nivel y la dirección de la relación que pueda existir entre dos o más variables
específicas, utilizando las respuestas dadas por los participantes.
Ramos-Galarza enfatiza que el objetivo de la investigación con alcance
correlacional es "determinar el grado de conexión entre las variables; al
saber los valores de una, se pueden prever, hasta cierto punto, los de la otra,
aunque no signifique que haya una relación causal" (2020, p. 3). Este
diseño, por ende, tiene como objetivo detectar patrones de asociación
significativos, sin buscar establecer conexiones causales directas.
Por último, el método hipotético-deductivo será el centro de análisis e interpretación de la evidencia. Este procedimiento supone la creación de hipótesis (que provienen de teorías o de observaciones iniciales), las cuales serán comparadas a través de métodos estadísticos. La verificación o negación de las hipótesis propuestas se realizará mediante el uso estricto de la estadística, lo que proporcionará la solidez empírica requerida para alcanzar la consistencia científica del estudio. En síntesis, la articulación coherente del paradigma positivista, el enfoque cuantitativo, el diseño correlacional y el método hipotético-deductivo proporciona un marco metodológico sólido para alcanzar las metas y garantizar la confiabilidad de los hallazgos.
RESULTADOS Y DISCUSIÓN
El primer paso esencial para mostrar y apoyar los hallazgos de la investigación actual fue garantizar que el instrumento de recolección de datos usado fuera confiable. Se entiende por confiabilidad a la capacidad de un instrumento para generar resultados consistentes y estables a través del tiempo y entre los distintos grupos analizados; esta condición es esencial para asegurar la calidad de los datos obtenidos y, en consecuencia, la validez de las conclusiones que se desprenden del estudio. El Coeficiente Alfa de Cronbach fue utilizado para llevar a cabo esta evaluación. Este es un método estadístico que se usa mucho en estudios cuantitativos, sobre todo cuando se emplean escalas de tipo Likert. El coeficiente permite determinar el grado de consistencia interna que hay entre los ítems que se han creado para evaluar una misma dimensión o constructo.
El coeficiente Alfa de Cronbach se representa en una escala que va del 0 al 1, la interpretación de este valor se lleva a cabo de la siguiente manera: se acepta cualquier valor que esté por encima de 0.70. Una consistencia interna de calidad se refleja en valores mayores a 0.80, los valores cercanos o superiores a 0.90 indican una fiabilidad del instrumento excelente. La Tabla 1 presenta el resultado de esta evaluación, que muestra el coeficiente Alfa de Cronbach obtenido para todos los ítems examinados.
Tabla 1: Alpha de Cronbach
|
Estadísticas de fiabilidad |
|
|
Alfa de Cronbach |
N de elementos |
|
,933 |
18 |
Se llevó a cabo el análisis de fiabilidad del instrumento para la recolección de datos, que constó de una escala Likert con 18 elementos, utilizando el Coeficiente Alfa de Cronbach, este es fundamental para evaluar la consistencia interna y garantizar que los ítems están correlacionados correctamente para examinar un constructo teórico de manera uniforme. Según se muestra en la Tabla 1, el valor total de los ítems evaluados fue de .933. Como este valor es mayor que .90, la investigación avala una excelente fiabilidad del instrumento, lo que valida la calidad metodológica del estudio.
La elaboración de baremos normativos fue necesaria para clasificar el rendimiento de los participantes en comparación con el grupo de referencia (N=119), y esto sirvió como base para interpretar las variables Habilidad para Resolver Problemas (HRP), Comprensión Conceptual (CC) y Modelación Matemática (MM). Se eligió un método que se basa en el rango de puntos de la muestra, una perspectiva sólida que considera que la distribución se parece a la curva normal. Concretamente, las puntuaciones se dividieron en tres niveles: Bajo, que se refiere a las puntuaciones en el rango de 6 a 13; Alto, para aquellas que son más altas de 23; y Medio, para los valores que están entre ambos límites. Este sistema no solo asegura que la clasificación pueda replicarse, sino que también proporciona validez discriminativa al posibilitar la identificación exacta de los participantes con rendimientos extremos. La consistencia de estos baremos se comprobó a través de un análisis de frecuencias, lo que confirmó que la distribución de los casos en las categorías obtenidas coincide con las expectativas teóricas para la variable y ofrece así una base firme para la interpretación de los resultados.
Tabla 2. Baremos de cada variable distribuidos por carreras
|
|
Carrera que cursa: |
|||||||||||||
|
Administración de Empresas |
Contabilidad y Auditoría |
Mercadotecnia |
Total N |
Porcentaje |
Total % |
|||||||||
|
Recuento |
Recuento |
Recuento |
||||||||||||
|
Modelación Matemática |
Bajo |
1 |
1 |
1 |
3 |
2,52 |
100 |
|
||||||
|
Medio |
26 |
21 |
17 |
64 |
53,78 |
|
||||||||
|
Alto |
27 |
15 |
10 |
52 |
43,7 |
|
||||||||
|
Compresión Conceptual |
Bajo |
5 |
1 |
0 |
6 |
5,04 |
100 |
|
||||||
|
Medio |
25 |
24 |
19 |
68 |
57,14 |
|
||||||||
|
Alto |
24 |
12 |
9 |
45 |
37,82 |
|
||||||||
|
Habilidad de Resolver Problemas |
Bajo |
7 |
7 |
2 |
16 |
13,45 |
100 |
|
||||||
|
Medio |
31 |
25 |
19 |
75 |
63,03 |
|
||||||||
|
Alto |
16 |
5 |
7 |
28 |
23,52 |
|
||||||||
En la Tabla 2, se realiza el estudio de la repartición de competencias como la Habilidad de Resolver Problemas, Comprensión Conceptual y Modelación Matemática por carrera muestra que los patrones de rendimiento son diversos y sugiere una relación entre el nivel de habilidad y la carrera. Con un tamaño de muestra de N=119, se nota que los niveles medios que son más del 53% en todas las competencias son más frecuentes que los niveles altos y bajos. En particular, la Modelación Matemática y la Comprensión Conceptual tienen el porcentaje más alto de estudiantes, mientras que en el nivel Alto existe un 43.7% y 37.82%, respectivamente, a diferencia de la Habilidad de Resolver Problemas, que es la menos fuerte, con únicamente un 23.52% de los estudiantes en el nivel Alto y siendo predominante el medio con un 63.03%. Cuando se desagrega por carrera, los estudiantes de Administración de Empresas muestran invariablemente el mejor rendimiento relativo, acumulando la mayor parte de los casos en el nivel Alto para las tres habilidades (27 en MM, 24 en CC y 16 en HRP). Por el contrario, los estudiantes de Contabilidad y Auditoría tienen la mayor debilidad en la Habilidad de Resolver Problemas, con la cifra más baja en el nivel Alto (5) y la misma cantidad que Administración de Empresas en el nivel Bajo (7), lo cual corrobora que esta carrera podría necesitar una intervención específica. En conclusión, los alumnos de Mercadotecnia se agrupan mayoritariamente en el nivel Medio en todas las competencias, con escasa representación en los niveles Bajo y Alto.
Después de haber establecido la solidez del instrumento, se procederá a analizar la normalidad de los datos para identificar la prueba de correlación adecuada y luego examinar las correlaciones entre los ítems. La normalidad de los datos es un supuesto esencial en la estadística inferencial, ya que su cumplimiento es el elemento crucial para determinar qué pruebas se utilizarán y si son válidas. El propósito principal de este análisis es comprobar si la distribución que se observa en nuestra muestra se parece con razonabilidad a la curva teórica de distribución normal. Es crucial atenerse a este supuesto: si los datos tienen una distribución normal, se prefiere utilizar pruebas paramétricas, que son más potentes por naturaleza para identificar diferencias o vínculos. En cambio, si existe una desviación importante de la normalidad, es necesario elegir las pruebas no paramétricas. Aunque estas últimas son más flexibles en lo que respecta a sus requerimientos de distribución, generalmente tienen menor eficiencia en su habilidad para detectar estadísticamente. Para realizar esta verificación, se utilizan pruebas particulares como la de Kolmogorov-Smirnov o la de Shapiro-Wilk. Debido a que la muestra empleada en esta investigación excede los 50 casos, se eligió la prueba de Kolmogorov-Smirnov. El criterio de decisión es el mismo: la normalidad solo se tiene en cuenta si el valor p-valor obtenido es más alto que el nivel de significancia, que es 0.05.
Tabla 3. Prueba de Normalidad de los datos
|
|
Kolmogorov-Smirnova |
||
|
Estadístico |
gl |
Sig. |
|
|
Modelación Matemática |
,122 |
119 |
,000 |
|
Comprensión Conceptual |
,131 |
119 |
,000 |
|
Habilidad de Resolver Problemas |
,139 |
119 |
,000 |
La prueba de Kolmogorov-Smirnov (K-S) se utilizó para evaluar el análisis de normalidad, que es esencial para aplicar pruebas paramétricas, por el tamaño de la muestra (N=119). Para las tres competencias analizadas, los resultados de la Tabla 3, señalan que es necesario rechazar la hipótesis nula (Ho), que propone que la distribución es normal. El nivel de significancia para la modelación matemática (sig. = 0.000), la comprensión conceptual (Sig. = 0.000) y la Habilidad de Resolver Problemas (Sig. = 0.000) es menor que el α = 0.05. Esta prueba estadística concluyente muestra que las puntuaciones de las tres variables no se distribuyen de manera normal. esas pruebas no dependen del supuesto de normalidad y son más sólidas para datos obtenidos mediante escalas Likert.
A continuación, se pretende determinar la validez estructural del instrumento, evaluando su consistencia interna a través de un análisis de los vínculos estadísticamente significativos entre los diferentes ítems que lo constituyen. Con este objetivo, se utilizará el coeficiente de correlación de Spearman, un método comúnmente utilizado en la investigación cuantitativa. Este procedimiento es fundamental para identificar patrones de asociación o disociación entre las variables, lo cual nos posibilita deducir la robustez del constructo que se está evaluando. Un estudio minucioso de estas correlaciones no solo descubre ítems que se alejan de la dimensión principal o posibles redundancias entre reactivos, sino que además hace más fácil el reconocimiento de elementos que podrían estar evaluando un factor distinto al teorizado en primer lugar. A partir de estos descubrimientos, se podrán tomar decisiones fundamentadas sobre la revisión de la redacción, la reestructuración conceptual o la depuración final del instrumento. La tabla 4 que se muestra a continuación expone los hallazgos más importantes del análisis, resaltando las conexiones con una asociación de mayor tamaño, porque son las más significativas para respaldar la validez interna.
Tabla 4. Correlación entre las variables
|
|
Modelación Matemática |
Comprensión Conceptual |
Habilidad de Resolver Problemas |
||
|
Rho de Spearman |
Modelación Matemática |
Coeficiente de correlación |
1,000 |
,751** |
,499** |
|
Sig. (bilateral) |
. |
,000 |
,000 |
||
|
N |
119 |
119 |
119 |
||
|
Comprensión Conceptual |
Coeficiente de correlación |
,751** |
1,000 |
,539** |
|
|
Sig. (bilateral) |
,000 |
. |
,000 |
||
|
N |
119 |
119 |
119 |
||
|
Habilidad de Resolver Problemas |
Coeficiente de correlación |
,499** |
,539** |
1,000 |
|
|
Sig. (bilateral) |
,000 |
,000 |
. |
||
|
N |
119 |
119 |
119 |
||
|
**. La correlación es significativa en el nivel 0,01 (bilateral). |
|||||
El
coeficiente Rho de Spearman 
se utilizó para estudiar la correlación entre las
tres competencias, y los resultados mostraron que todas las variables están
interrelacionadas de manera positiva y significativa a un nivel 
, lo que brinda una fuerte prueba de la validez estructural interna del
constructo general de competencias. La conexión más sólida se encuentra entre
la Modelación Matemática y la Comprensión Conceptual (
, 
), lo que sugiere que estas competencias son muy
dependientes entre sí o muestran un mismo centro de razonamiento abstracto. Por
otro lado, la Comprensión Conceptual tiene una correlación significativa y
fuerte con la Habilidad para Resolver Problemas ((
, ), lo que indica que la base teórica es un predictor
importante de la aplicación práctica, pero no el único. La correlación más
débil de la matriz se establece entre Habilidad de Resolver Problemas y
Modelación Matemática ((
, ). Aunque el valor es significativo, está cerca de la
correlación moderada y sugiere que la habilidad para solucionar problemas
prácticos incluye elementos extra que exceden lo estrictamente matemático, como
puede ser el juicio al tomar decisiones o la capacidad creativa. En general,
estos hallazgos corroboran que las tres variables evalúan un conjunto de
destrezas coherente, aunque subrayan una autonomía conceptual superior en la
habilidad de resolver problemas.
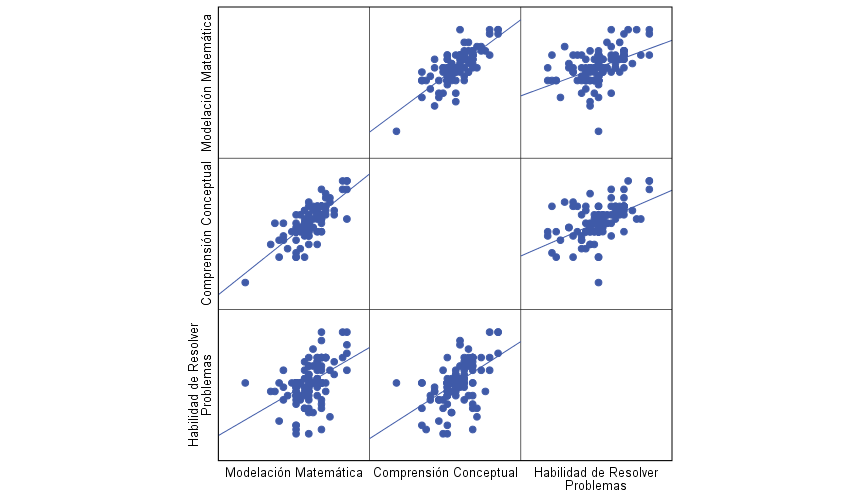
Fig. 1: Grafica de dispersión de las correlaciones
Por
último, en la Fig. 1 se muestra una matriz de correlaciones gráficas, donde corrobora
la validez interna estructural, al mostrar relaciones positivas y
significativas entre cada una de las variables. La correlación más fuerte fue
entre la Comprensión Conceptual y la Modelación Matemática ( ), en tanto que la más débil () con la Habilidad de Resolver Problemas, lo cual
indica que esta última es una habilidad más independiente y necesita factores
extra para su dominio que no son exclusivamente matemáticos.
CONCLUSIÓN
Los estudiantes muestran un rendimiento moderado en las competencias como la Habilidad de Resolver Problemas, Comprensión Conceptual y Modelación Matemática; esto sugiere que existe un espacio considerable para mejorar el currículo. La Habilidad de Resolver Problemas es la que más debilidades presenta, no solamente tuvo el promedio más bajo apenas encima de la neutralidad, sino que también mostró la dispersión más alta, lo cual indica una gran variabilidad en el manejo práctico del saber. Desde el punto de vista metodológico, la prueba de Kolmogorov-Smirnov rechazó la hipótesis de normalidad en todas las variables, lo que confirma el empleo de pruebas no paramétricas para todas las inferencias y garantiza la solidez de las comparaciones entre los grupos.
El análisis de correlación de Spearman corroboró una sólida validez estructural interna, dado que todas las competencias están interrelacionadas de manera significativa y positiva; esto indica que evalúan un constructo consistente de capacidad analítica. Sin embargo, la intensidad de las relaciones varía, y es importante señalar que la dimensión más autónoma del constructo es la Habilidad de Resolver Problemas, lo que significa que su dominio necesita factores adicionales además de la comprensión o modelado simplemente teóricos. En el análisis de contingencia por carrera, esta debilidad estructural se acentúa. En este análisis, los estudiantes de Contabilidad y Auditoría evidencian la mayor fragilidad en la Habilidad de Resolver Problemas, mientras que Administración de Empresas exhibe el rendimiento más firme. Por ende, cualquier táctica educativa debe ser distinta y dar prioridad a una intervención centrada en las competencias de aplicación práctica para la carrera de Contabilidad y Auditoría.
AGRADECIMIENTOS
Queremos manifestar nuestro más profundo agradecimiento a los estudiantes de la Facultad de Ciencias Administrativas y Económicas de la Universidad Técnica del Norte por su colaboración y participación en este estudio, contribuyendo con sus recursos, espacios y conocimientos que mejoraron notablemente esta investigación. De igual manera un agradecimiento de manera especial a nuestras familias, que han sido un soporte esencial durante todo este proceso. Gracias a su apoyo sin condiciones, comprensión y constante estímulo, se logró completar esta investigación.
REFERENCIAS
Duarte, J., & Cárdenas, S. (2024). Meta-Análisis de la Modelación Matemática: Un Tamaño del Efecto de $d = 0.65$ en Habilidades Superiores. Review of Educational Research, 94(2), 200–225. doi: 10.3102/00346543231215432
Fuentes, A., & Herrera, G. (2023). Evaluación de la Habilidad de Solución de Problemas mediante Modelos Matemáticos. Journal of Mathematics Education, 18(2), 200–215. doi:10.12973/ajme.2023.18200a
García, A., & Pérez, M. (2021). Aplicación de la Modelación en la Ingeniería: De la Teoría a la Praxis. Journal of Applied Mathematical Education, 15(3), 112–129. doi: 10.1016/j.jame.2021.03.005
Hernández-Sampieri, R., & Mendoza, C. P. (2020). Metodología de la investigación: Las rutas cuantitativa, cualitativa y mixta. McGraw Hill.
Jiménez, R., & Núñez, H. (2022). Modelación y Pensamiento Crítico: Un Estudio Longitudinal en Educación Media y Superior. Thinking Skills and Creativity, 46, 101200. doi: 10.1016/j.tsc.2022.101200
Landaluce, M. I. (2024). Recodificación de escalas tipo Likert a través de la clasificación no supervisada. Las implicaciones de las relaciones por Internet respecto a las relaciones presenciales como estudio de caso. Revista Internacional de Sociología, 82(2), e251. https://doi.org/10.3989/ris.2024.82.2.M23-06
López, E., Torres, L., & Bermejo, I. (2020). Modelación Matemática como Herramienta Transversal en la Educación Superior. Contemporary Educational Research, 45(1), 50–68. doi: 10.1080/13598139.2020.1789012
Martínez, F., & Bravo, L. (2023). Impacto de Metodologías Activas en la Transferencia de Conocimiento Universitario. International Journal of Science and Mathematics Education, 21(5), 901–920. doi: 10.1007/s10763-023-10333-z
Méndez, H., Gil-Madrona, P., & Martínez-Fernández, R. (2021). Medición en investigación a través de Escalas Likert: teoría y práctica. Revista de Ciencias Sociales, 2(1), 30–45.
Morales, P., & Rojas, H. (2020). Análisis de Competencias de Modelación en Egresados de Ingeniería: El Déficit del 65%. Journal of Professional Education, 50(4), 412–430. doi: 10.1108/jpe-03-2020-0034
Pérez, D., & Díaz, A. (2020). Medición del Impacto de la Modelación Matemática en la Comprensión a Nivel de Grado. Studies in Higher Education, 45(8), 1690–1705. doi: 10.1080/03075079.2020.1712345
Quintero, N., & Rojas, F. (2024). Reforma Curricular Basada en Modelación Matemática: Una Perspectiva Global. Teaching and Teacher Education, 137, 104432. doi: 10.1016/j.tate.2024.104432
Ramírez, C., & Soto, P. (2022). Competencias del Siglo XXI: El Papel de la Traducción Matemática. Higher Education Studies, 12(4), 1-15. doi: 10.5430/hes.v12n4p1
Ramos-Galarza, C. A. (2020). Los alcances de una investigación. CienciAmérica, 9(3), 1–6. https://doi.org/10.33210/ca.v9i3.336
Silva, J., Acosta, R., & Vidal, M. (2021). Efectos Cognitivos de la Modelación en la Adquisición de Conceptos Científicos. Educational Research Review, 34, 100345. doi: 10.1016/j.edurev.2021.100345
Valarezo, D. D., Lema, L. S., & Paguay, S. F. (2020). El positivismo. Revista Arbitrada Interdisciplinaria de Ciencias Sociales. Ciencia Latina, 4(3), 265-278. https://doi.org/10.37811/cl_raciso.v4i3.136
Vega, S., & Castro, D. (2024). Necesidad de Evidencia Cuantitativa de la Modelación Matemática en Contextos Universitarios. European Journal of Educational Psychology, 15(1), 1-20. doi: 10.1080/23328574.2024.2301234