La enseñanza matemática en la educación secundaria: Consideraciones en los adolescentes

Mathematics teaching in secondary education: Considerations for adolescents

Heimdal Humberto Gómez Ramírez¹

¹Investigador independiente, heimdalgomez@hotmail.com, https://orcid.org/0009-0009-7276-824X, México

	Información del Artículo	RESUMEN
	Trazabilidad: Recibido 01-12-2024 Revisado 02-12-2024 Aceptado 08-12-2024	La enseñanza de las matemáticas abarca estrategias pedagógicas que fomenten el aprendizaje significativo y el desarrollo de competencias matemáticas. La práctica docente se centra en un modelo en el que el profesor actúa como facilitador, estimulando la curiosidad y el amor por el aprendizaje mediante metodologías como la resolución de problemas, que abordan la identificación, análisis, desarrollo y evaluación de soluciones, relacionadas con la vida cotidiana. La didáctica de las matemáticas ha evolucionado hacia una disciplina científica que fomenta aprendizajes significativos mediante experiencias reales y el uso de los conocimientos previos del alumno. En esta investigación, aplicada a dos grupos de primer grado, se emplea el instrumento de inteligencias múltiples de Gardner para identificar fortalezas cognitivas, personalizar estrategias y mejorar la interpretación de resultados. Los hallazgos destacan la necesidad de adaptar las metodologías de enseñanza a las inteligencias predominantes para optimizar el aprendizaje matemático.
	Palabras Clave: Enseñanza Matemáticas Adolescente
Keywords: Teaching Mathematics Teenager		ABSTRACT Mathematics teaching encompasses pedagogical strategies that foster meaningful learning and the development of mathematical skills. Teaching practice focuses on a model in which the teacher acts as a facilitator, stimulating curiosity and a love of learning through methodologies such as problem solving, which address the identification, analysis, development and evaluation of solutions related to everyday life. Mathematics teaching has evolved into a scientific discipline that fosters meaningful learning through real experiences and the use of students' prior knowledge. In this research, applied to two first grade groups, Gardner's multiple intelligences instrument is used to identify cognitive strengths, personalize strategies and improve the interpretation of results. The findings highlight the need to adapt teaching methodologies to the predominant intelligence to optimize mathematical learning.

INTRODUCCIÓN

La realización de la presente investigación exige una profunda comprensión de los componentes esenciales de la investigación científica y como primer elemento el contexto del problema es fundamental. Este planteamiento constituye un punto crucial para justificar el propósito de la investigación. En consecuencia, una investigación se origina a partir de la observación que genera una idea que constantemente relacionamos con la realidad. Por lo tanto, es esencial respaldar esta perspectiva con un papel determinante que explica la problemática que el investigador está abordando y su deseo de descubrir lo que parece ser una situación desconocida pero desafiante hasta el momento. Debido a lo anterior, la labor docente juega un papel fundamental en la ejecución de este proyecto.

A lo largo de los años, la práctica docente ha experimentado una evolución constante con el propósito de mejorar la calidad de la enseñanza y el proceso de aprendizaje de los estudiantes. En el contexto de la educación secundaria, las matemáticas también han experimentado cambios a lo largo del tiempo. Por tanto, es relevante destacar la evolución de la educación secundaria y de la enseñanza de las matemáticas hasta la actualidad, ya que este marco histórico constituye el entorno en el que se desarrollará nuestra investigación.

MATERIALES Y MÉTODOS

Metodología de la investigación.

En la investigación científica de cualquier tipo es un requerimiento esencial el marco metodológico Este componente es esencial para dotar de coherencia y relevancia al estudio, ya que exhibe los elementos sistemáticos y organizados que sustentan y vinculan a la investigación en cuestión. En este contexto, el marco metodológico se erige como el momento propicio para presentar las técnicas, estrategias y métodos que facilitarán la verificación de nuestras teorías y supuestos. Su finalidad última es analizar y contribuir al conocimiento del campo de estudio en el que nos adentramos. Al respecto Azuero menciona:

La formulación del marco metodológico en una investigación es permitir, descubrir los supuestos del estudio para reconstruir datos, a partir de conceptos teóricos habitualmente operacionalizados. Significa detallar cada aspecto seleccionado para desarrollar dentro del proyecto de investigación que deben ser justificado por el investigador. Respaldado por el criterio de expertos en la temática, sirviendo para responder al “como” de la investigación. Se expone el tipo de datos que se requiere buscar para dar respuesta a los objetivos, así como la debida descripción de los diferentes métodos y técnicas que se emplearan para obtener la información necesaria. (2019, p. 1)

Por lo tanto, este apartado tiene como objetivo principal respaldar de manera explícita los mecanismos metodológicos e instrumentos empleados durante la investigación desarrollada en este trabajo de tesis. En este mismo apartado, se incorporan los instrumentos que detallan las variables clave de la investigación, sus teorías, dimensiones e indicadores esenciales. Todo esto se realiza con el propósito de abordar de manera integral la problemática que atañe a la presente investigación.

Enfoque de la investigación.

Con el propósito de validar el abstracto preestablecido y alcanzar los objetivos propuestos en esta investigación, se ha decidido adoptar un enfoque metodológico cuantitativo. Este enfoque se selecciona con la intención de medir de manera precisa la realidad o fenómeno de estudio. Como lo menciona Avalos:

Este enfoque implica el uso de herramientas matemáticas y estadísticas para llegar a resultados. Estos datos permiten identificar asociaciones explicativas o relaciones causales entre variables. Los trabajos de investigación bajo este enfoque cuantifican variables, las mismas que serán observadas, descritas, medidas o sometidas a alguna experimentación controlada. (2021, p. 338)

Para la recolección de datos se ha optado por determinadas técnicas, y el método elegido es la realización de encuestas, para ello utilizaremos un instrumento basado en la escala Likert. El objetivo detrás de esto es realizar un análisis exhaustivo y un procesamiento estadístico de los datos que se han recopilado. Al hacerlo, podremos abordar la pregunta de investigación en cuestión y poner a prueba el abstracto formulada.

Enseñanza de las matemáticas.

La enseñanza de las matemáticas abarca el conjunto de estrategias, métodos y enfoques utilizados por los docentes para impartir los contenidos matemáticos a los estudiantes de primer grado de secundaria. Esto implica no solo la transmisión de conocimientos sino también la adopción de prácticas pedagógicas que promuevan el interés, la participación y la comprensión profunda de los conceptos matemáticos. A continuación, se enlistan los indicadores que darán soporte al indicador de la enseñanza de las matemáticas:

1. La escuela secundaria

2. La práctica docente.

3. Didáctica de las matemáticas.

4. Metodología de la enseñanza de las matemáticas.

I. Escuela Secundaria

La etapa de la escuela secundaria marca un período crucial en el proceso de maduración y en la adquisición de diversas experiencias por parte de los adolescentes, las cuales contribuyen significativamente a su desarrollo personal. Esta formación se ve respaldada por una variedad de cursos que los estudiantes cursan durante este tiempo. Entre estos, las matemáticas desempeñan un papel fundamental al potenciar diversas competencias a través de contenidos especializados. Algunas de estas competencias incluyen:

· Desarrollo de formas de pensamiento para formular conjeturas y procedimientos de resolución de problemas, así como la capacidad de elaborar explicaciones para fenómenos numéricos o geométricos específicos.

· Utilización de diversas técnicas y recursos con el fin de optimizar los procedimientos de resolución, fomentando así la eficiencia en el abordaje de los desafíos matemáticos.

· Demostración de disposición hacia el estudio de las matemáticas, así como hacia el trabajo autónomo y colaborativo. Este enfoque no solo promueve el desarrollo individual, sino que también facilita el aprendizaje mediante la interacción y colaboración con otros compañeros.

En resumen, las matemáticas durante la educación secundaria no solo se centran en la transmisión de conocimientos, sino que también buscan cultivar habilidades cognitivas, actitudes positivas hacia el aprendizaje y la disposición para trabajar de manera independiente y en equipo.

En México, la educación secundaria ha experimentado una transformación significativa con la introducción de los nuevos planes y programas de estudios de 2022, conocidos como "La nueva escuela mexicana". Este cambio se implementará plenamente en el ciclo escolar 2023-2024, abarcando los tres grados de la secundaria, correspondientes a la fase 6. En este innovador plan de estudios, es relevante destacar que las tradicionales asignaturas ahora son denominadas disciplinas. Anteriormente, estas disciplinas estaban divididas en tres campos formativos, y la materia de matemáticas se ubicaba en el "campo de formación académica". En contraste, en el plan de 2022, la organización se ha reestructurado en campos formativos, situando la disciplina de matemáticas en el área de "saberes y pensamiento científico", el campo de saberes y pensamiento científico en el plan de estudios 2022 se describe por la Secretaría de Educación Pública como:

El objeto de aprendizaje de este campo es la comprensión y explicación de los fenómenos y procesos naturales tales como el cuerpo humano, los seres vivos, la materia, la energía, la salud, el medio ambiente y la tecnología, desde la perspectiva de diversos saberes y en su relación con lo social, articulando el desarrollo del pensamiento matemático a este fin. En este marco, el pensamiento científico representa un modo de razonamiento que implica relaciones lógicas de conocimientos fundados en el desarrollo de habilidades para indagar, interpretar, modelizar, argumentar y explicar el entorno. Lo anterior se articula con el desarrollo del pensamiento matemático, abriendo paso a organizar la ciencia/matemática escolar desde la interpretación de fenómenos y la resolución de problemas complejos. En este sentido, se plantea como reto la posibilidad de articular en el aula las ideas científicas y las matemáticas, para dotar a los alumnos de herramientas conceptuales para enfrentar los complejos problemas del mundo actual. (2023, p.54)

Este cambio no solo refleja una reorganización conceptual, sino también una adaptación curricular que busca alinear la educación secundaria con los principios y objetivos de "La nueva escuela mexicana". La redefinición de las disciplinas y su reubicación en campos formativos específicos refleja una aproximación más integrada y holística para potenciar el desarrollo académico y científico de los estudiantes en este nivel educativo.

Para ello también es importante mencionar las especificidades del campo formativo que hacen hincapié en elementos fundamentales del desarrollo de autonomía. La Secretaría de Educación Pública menciona que la especificidad del campo:

Busca fortalecer el pensamiento científico, entendido como una manera de razonar que implica establecer relaciones coherentes de conocimientos fundados en el desarrollo de habilidades para indagar, interpretar, argumentar y explicar el entorno e incidir en problemáticas relevantes de la comunidad, considerando la objetividad, racionalidad y sistematicidad en la construcción de modelos y del lenguaje propios de la ciencia (2023, p.56).

Es importante también señalar la finalidad del campo formativo, ya que está estrechamente relacionado con el fomento de la autonomía durante la trayectoria educativa del estudiante en la educación básica. La Secretaría de Educación Pública menciona que la finalidad del campo:

· Comprendan y expliquen procesos y fenómenos naturales en su relación con lo social a partir de la indagación; interpretación; experimentación; sistematización; identificación de regularidades; modelación de proceso y fenómenos; argumentación; formulación y resolución de problemas; comunicación de hallazgos; razonamiento y; formulación, comparación y ejercitación de procedimientos y algoritmos.

· Consideren el lenguaje científico y técnico como forma de expresión oral, escrita, gráfica y digital para establecer nuevas relaciones, construir conocimientos y explicar modelos.

· Reconozcan y utilicen diversos métodos en la construcción de conocimientos, para contrarrestar la idea de un método único, tales como inductivo, deductivo, analítico, global, entre otros.” (2023, p.54).

No obstante, en la actualidad, nos enfrentamos a estudiantes de secundaria que se encuentran alejados de estos estándares y de los propósitos que el plan y programas buscan inculcar en ellos, la brecha entre las expectativas del plan de estudios y la situación real en las aulas destaca la necesidad de abordar de manera efectiva el proceso de aprendizaje autónomo, este proceso implica empoderar a los estudiantes para que asuman un papel activo en su educación, tomando la iniciativa en la búsqueda de conocimiento, la resolución de problemas y el desarrollo de habilidades autodidactas.

II. Práctica docente.

La práctica docente, como su nombre indica, se centra en el profesor y en la forma en que desarrolla su labor para impartir una clase. Involucra no solo la manera en que se comunica, sino también su comportamiento, relaciones interpersonales, planificación y, en última instancia, todos los aspectos que contribuyen a la enseñanza. En otras palabras, la práctica docente abarca las acciones y estilos adoptados por el docente, los cuales están inevitablemente influenciados por el contexto en el que se desenvuelve.

Sin embargo, no se debe dejar de lado que la práctica docente involucra dos actores, el estudiante y el docente y este último debe ser un especialista en la materia que enseña, pero, además, debe ser un especialista en la metodología de la enseñanza de esa disciplina, lo cual incluye conocimientos de díselo y desarrollo curricular, diseño y uso de medios y materiales de instrucción, por fin, métodos y técnicas de evaluación de los aprendizajes. Por ello, en el ámbito del aprendizaje, es esencial considerar que el principal objetivo de un maestro comprometido debe ser estimular la curiosidad, el disfrute, el amor, la pasión y el deseo de aprender. Una vez despiertos estos elementos, surgen naturalmente los conceptos, las definiciones, los esquemas y las clasificaciones, en resumen, las teorías y las abstracciones. La labor del profesor es sumamente compleja, ya que se ven influenciados por numerosos factores que inciden en su desempeño. Por ende, se requiere un compromiso significativo para facilitar el desarrollo y formación integral del estudiante.

III. Didáctica de la matemática

La didáctica constituye la materia prima fundamental para todo docente, ya que es crucial comprender qué procesos, elementos, estilos, teorías y métodos son los más apropiados para materializar un proceso de enseñanza efectivo en los estudiantes. Es relevante abordar la didáctica específica de la especialidad, pero aún más importante es analizar su evolución a lo largo del tiempo. Este análisis nos permite entender los cambios que ha experimentado y evaluar si hemos progresado y adaptado de manera adecuada a nuestro contexto las diversas formas de enseñar las matemáticas.

La didáctica de las matemáticas ha experimentado una evolución notable, transformándose de una necesidad básica en una disciplina científica que, a su vez, se ha convertido en una pedagogía particular. Este proceso se remonta a la antigüedad, cuando las matemáticas surgieron y se desarrollaron a partir de necesidades fundamentales, como el contar, repartir, sumar, entre otras. A lo largo de la historia, este conocimiento matemático evolucionó, pasando de ser una habilidad individual a la necesidad de compartir y enseñar estos conocimientos a otros, dando así origen a la didáctica de las matemáticas. En la actualidad, este proceso se refleja en la interacción entre el estudiante, deseoso de aprender, y el profesor, experto en la materia.

 El docente se enfrenta al desafío de buscar estrategias y métodos que faciliten al alumno la adquisición de esta ciencia. En este contexto, la didáctica de las matemáticas se convierte en un puente esencial, donde la enseñanza se adapta a las necesidades y capacidades del estudiante, promoviendo un aprendizaje efectivo y significativo.

La Didáctica Clásica, se centra en la enseñanza y el aprendizaje de las matemáticas como objetos didácticos, sin cuestionar el conocimiento a enseñar y considerándolo no problemático en sí mismo.

Para superar las limitaciones de la Didáctica Clásica, se ha evolucionado hacia la construcción de una disciplina científica que brinde explicaciones más sólidas para los problemas que surgen al introducir el conocimiento experto en las instituciones educativas para ser enseñado.

La didáctica fundamental aborda los objetos paracientíficos y sostiene que los fenómenos didácticos tienen un componente matemático esencial, siendo este un punto clave para el análisis didáctico. Esto implica que los conceptos matemáticos y los didácticos están intrínsecamente entrelazados en la construcción de la teoría didáctica, ya que lo didáctico está presente en todos los aspectos del proceso de estudio de las matemáticas. 

La didáctica de la matemática se ve desafiada a cuestionar el conocimiento matemático en sí mismo, así como los conceptos provenientes de disciplinas como la psicología o la sociología, que anteriormente se utilizaban y que ahora se convierten en objetos de estudio de esta disciplina, ampliando así el campo de la problemática didáctica. Su objeto de estudio es el proceso de estudio, y su metodología se basa en el análisis didáctico a partir del conocimiento matemático existente. A diferencia de la didáctica clásica, utiliza los conocimientos previos de los alumnos como punto de partida para el estudio de las situaciones, considerándolos como modelos de la actividad matemática.

El objeto de estudio de la didáctica de matemáticas es la situación didáctica, definida por Godino como:

Un conjunto de relaciones establecidas explícita y/o implícitamente entre un alumno o un grupo de alumnos, un cierto medio (que comprende eventualmente instrumentos u objetos) y un sistema educativo (representado por el profesor) con la finalidad de lograr que estos alumnos se apropien de un saber constituido o en vías de constitución (2020, p.149).

Es por ello por lo que, en la actualidad, se busca aplicar las matemáticas en el contexto de experiencias o situaciones reales para los alumnos, con el objetivo de lograr una comprensión más profunda y captar su atención de manera efectiva. Iniciar con ejemplos sencillos en los cuales los alumnos participen activamente ayuda a eliminar el temor a expresar opiniones en la clase de matemáticas, desmitificando la idea de que cometer errores es mal visto.

Al observar la evolución de los roles en la didáctica de las matemáticas, el profesor asume la función de un acompañante que brinda apoyo y guía a los estudiantes en la formalización del conocimiento matemático. Esta perspectiva refleja un cambio hacia un enfoque más colaborativo y facilitador, donde el maestro se convierte en un facilitador del aprendizaje, fomentando la participación y el desarrollo del pensamiento crítico en los estudiantes.

IV. Metodología en la enseñanza de las matemáticas.

Partiremos de mencionar que la metodología hace referencia al conjunto de procedimientos racionales utilizados para alcanzar algún objetivo; entonces la metodología en la enseñanza hace referencia al conjunto de procedimientos, estrategias las cuales buscan como fin el aprendizaje de un contenido.

En el ámbito de las matemáticas, diversas metodologías pueden aplicarse para alcanzar los objetivos de aprendizaje relacionados con competencias específicas o contenidos particulares. Sin embargo, es fundamental tener en cuenta diversos factores que pueden influir en la efectividad de estas metodologías, como el contexto en el que se desarrolla la enseñanza y la predisposición de los alumnos hacia determinadas prácticas. La resistencia al cambio o la falta de familiaridad con una nueva metodología pueden generar confusión e incluso desagrado por la clase, subrayando la importancia de abordar cuidadosamente cada enfoque.

En la investigación actual, se abordará la metodología recomendada en la nueva escuela, la cual es la resolución de problemas. A continuación, se ofrecerá una descripción detallada de esta metodología, así como una explicación de cómo se aplicará para el desarrollo del contenido.

Es importante mencionar que esta metodología es más eficaz si el alumno ve que el problema planteado es relacionado con su vida cotidiana; esto le llamara su atención además de que podrá entender de manera más fácilmente los contenidos marcados en el programa Esta metodología se divide en etapas las cuales se desarrollaran a continuación:

1. Identificación del problema.

La identificación del problema es una fase muy importante en la metodología, pues de ella depende el desarrollo interior en busca de la solución. Un problema bien delimitado es una gran ayuda para que el proceso general avance bien; un problema mal definido provocará desvíos conceptuales que serán difíciles de remediar posteriormente. En esta etapa es fundamental el análisis de la información inicial con el fin de distinguir los datos pertinentes de los que no lo son, de manera que se pueda elegir la configuración más conveniente respecto a las soluciones posibles. También deben definirse los datos de salida que garanticen la continuidad del proceso para que sea más fácil eliminar las expectativas negativas.

2. Planteamiento de alternativas de solución.

Después de la definición del problema y del análisis de los datos de entrada, el proceso continúa con el análisis de las alternativas de solución. Por lo general, la solución de un problema puede alcanzarse por distintas vías. Es útil tratar de plantear la mayor cantidad de alternativas posibles de solución, pues de esta forma las probabilidades aumentan a favor de encontrar la vía correcta. Se debe destacar que no es conveniente extender demasiado el número de alternativas, pues si el número de éstas es demasiado alto, se presentará una mayor dificultad para elegir la mejor de todas, que es en definitiva el objetivo del proceso.

3. Elección de una alternativa de una solución.

Después de tener todo el repertorio de alternativas, es necesario pasar a otra etapa: la elección de la mejor entre todas las posibilidades. Esta fase es muy importante porque de la elección realizada depende el avance final hasta la solución. La orientación hacia delante supone la irreversibilidad si la decisión es acertada o una "reversibilidad onerosa", pues si la decisión no es acertada, es necesario retroceder, lo que afecta la "optimidad" del proceso. Por lo tanto, es necesario que cada alternativa sea bien analizada para que la toma de decisiones sea bien justificada. Deberás elegir la alternativa que sea la más adecuada para la solución del problema, tomando en cuenta las características del problema y las características que deberá tener la solución, así como los elementos, datos o información con la que cuentas.

4. Desarrollo de la solución.

Después de decidir cuál es la mejor alternativa de todas, se llega a la etapa de la solución. En esta fase, a partir de los datos relacionados con la alternativa seleccionada, se aplican las operaciones necesarias para solucionar el problema. La selección de los procesos también debe ser determinada en función de la optimidad, es decir, las operaciones deben llegar a la solución por el camino más corto para garantizar la mayor eficiencia en el funcionamiento. Si la alternativa es la óptima, llevará a la solución deseada que fue prevista en la identificación del problema.

5. Evaluación de la solución.

Luego de haber desarrollado la solución queda aún una etapa, que es la evaluación. En los procesos industriales a este procedimiento se le llama control de la calidad y consiste en determinar que la solución obtenida 'es lo que se esperaba conseguir comprobando que el resultado sea correcto. En esta fase se deben "pulir" los procesos ya realizados y tratar de llevarlos a un grado mayor de optimidad, pues el algoritmo más eficiente en la solución de un problema es el que llega a su objetivo final con la mayor economía de procedimientos que sea posible. A continuación, puedes observar un ejemplo de la aplicación de la metodología a la solución de un problema simple. Es importante saber que los problemas complejos también se resuelven con esta estructura. 

RESULTADOS Y DISCUSIÓN

Esta investigación se desarrolla con dos grupos de primer grado de la Escuela Secundaria Técnica No.21, el primer grupo es 1°A que cuenta con 26 estudiantes de los cuales 11 son mujeres y 15 hombres que oscilan entre los 11 y 12 años, en cambio en el grupo de 1°B se encuentran inscritos 25 alumnos de los cuales son 12 mujeres y 13 hombres que tienen entre 11 y 12 años.

La aplicación del instrumento de inteligencias múltiples de Gardner en la investigación es una estrategia significativa. Este instrumento, desarrollado por Gardner, propone la existencia de diferentes tipos de inteligencias, reconociendo que las personas pueden tener fortalezas y preferencias en diversas áreas cognitivas. Al utilizar este instrumento, se busca obtener una comprensión más precisa de la forma de aprendizaje de los estudiantes, así como una delimitación más específica de su comportamiento en relación con las distintas inteligencias propuestas por Gardner. Al identificar las áreas en las que los estudiantes pueden destacar o presentar preferencias, se pueden relacionar estas variables con los objetivos y la metodología de la investigación. Algunos beneficios de utilizar el instrumento de inteligencias múltiples en este contexto incluyen:

· Adaptación de Estrategias Pedagógicas: La identificación de las inteligencias predominantes en los estudiantes puede informar a los docentes sobre las estrategias pedagógicas más efectivas para cada individuo.

· Personalización del Aprendizaje: Reconocer las fortalezas y preferencias en las inteligencias múltiples permite la personalización del proceso de aprendizaje, adaptando las actividades y el contenido para satisfacer las necesidades individuales de los estudiantes.

· Relación con la Metodología de la Investigación: Al relacionar las inteligencias múltiples con las variables de interés en la investigación, se puede obtener una comprensión más rica y contextualizada de cómo los estudiantes abordan la metodología propuesta y cómo se relaciona con su forma única de aprender.

· Mejor Interpretación de Resultados: La información obtenida a través del instrumento de inteligencias múltiples puede contribuir a una mejor interpretación de los resultados de la investigación, permitiendo una comprensión más completa de cómo las variables en estudio se manifiestan en la diversidad de estilos de aprendizaje.

Se presentarán los resultados mediante dos gráficas. La primera grafica exhibirá la cantidad de alumnos que han marcado alguna de las inteligencias previamente mencionadas. A continuación, se mostrará otra gráfica en la que se observará la relación entre la inteligencia y la cantidad de alumnos que la poseen de manera destacada. Este instrumento tiene como objetivo brindar apoyo en función de las inteligencias predominantes en la mayoría de los alumnos.

El instrumento se aplicó a ambos grupos siendo un total de 47 alumnos de un total de 51 de los cuales 23 pertenecen al 1°A y 24 alumnos perteneces al 1°B. Los resultados obtenidos en términos de preferencia neta para algún tipo de inteligencia son los siguientes:

Características del grupo de 1°A.

En esta investigación, resulta relevante destacar el horario en el cual los estudiantes reciben clases de matemáticas en la ubicación donde se lleva a cabo el estudio. En la tabla 4 se menciona el horario de clases del grupo de 1°A

Tabla 1: Horario clase de matemáticas de 1°A

Día	Hora
Lunes	11-10 am – 12:00 pm
Martes	9:00 am – 9:50 am
Miércoles	12:50 pm – 1:40 pm
Jueves	12:50 pm – 1:40 pm
Viernes	7:20 am – 8:10 am

A continuación, los resultados que se obtuvieron a partir del instrumento de inteligencias múltiples:

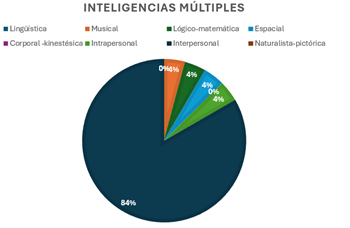
Fig. 1: Resultado 1°A inteligencias múltiples

En la gráfica 1 se observar que hubo un total de 23 alumnos que presentaron una inteligencia múltiple sobresaliente y/o marcada, 20 alumnos que representan el 84% mostraron tener la inteligencia interpersonal como tendencia, 1 alumno (4%) muestra la inteligencia intrapersonal como tendencia, 1 muestra la inteligencia lógico-matemáticas como tendencia y por último 1 alumno muestra la inteligencia musical-rítmica como tendencia. Estos resultados nos quieren decir que el grupo trabaja de una manera armónica entendiendo a cada uno de sus compañeros, además de que pueden relacionarse muy fácilmente con las demás personas; esto nos da pie a poder trabajar en equipos ya sea para exposiciones o ejercicios durante la clase.

Características del grupo de 1°B.

En esta investigación, resulta relevante destacar el horario en el cual los estudiantes reciben clases de matemáticas en la ubicación donde se lleva a cabo el estudio. En la tabla 5 se menciona el horario de clases del grupo de 1°B.

Tabla 2: Horario clase de matemáticas de 1°B

Día	Hora
Lunes	9:50 am – 10:40 pm
Martes	12:00 pm – 12:50 pm
Miércoles	12:00 pm – 12:50 pm
Jueves	11:10 am – 12:00 pm
Viernes	12:50 pm – 1:40 pm

A continuación, los resultados que se obtuvieron a partir del instrumento de inteligencias múltiples:

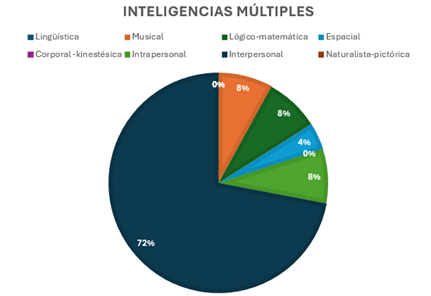
Fig. 2: Resultados 1°B inteligencias múltiples

En la gráfica 2 se observar que hubo un total de alumnos que presentaron una inteligencia múltiple sobresaliente y/o marcada, 18 alumnos que representan el 72% mostraron tener la inteligencia interpersonal como tendencia, 2 alumno (8%) muestra la inteligencia intrapersonal como tendencia, 2 muestra la inteligencia lógico-matemáticas tendencia y por último 2 alumno muestra la inteligencia musical-rítmica como tendencia. Estos resultados nos quieren decir que el grupo trabaja de una manera armónica entendiendo a cada uno de sus compañeros, además de que pueden relacionarse muy fácilmente con las demás personas; esto nos da pie a poder trabajar en equipos ya sea para exposiciones o ejercicios durante la clase.

Después de haber presentado cada uno de los resultados y los comportamientos observados en los grupos, es crucial contextualizar al estudiante como un adolescente. Esto permitirá prever y tener conciencia del comportamiento que puede manifestar. Para ello, nos respaldaremos en las significativas contribuciones de dos influyentes autores respecto a la adolescencia: Vygotsky y Piaget. Uno de los aspectos fundamentales que experimenta el adolescente en esta etapa es el proceso cognitivo. A continuación, se presentará un cuadro comparativo entre Piaget y Vygotsky para proporcionar una visión más detallada de sus respectivas teorías.

Tabla 3: Cuadro de desarrollo adolescente.

Piaget. Los estadios (Ser biológico).

Vigostky. Ser social.

Todos los seres humanos pasamos por estos estadios según Piaget, el ser humano no puede retroceder en el razonamiento ya adquirido, es decir, no puede reducirse su pensamiento formal. Es muy importante reconocer que empezamos estos estadios desde que nacemos y con ello vamos adquiriendo un mejor proceso cognoscitivo es decir vamos adquiriendo esquemas mentales, así como el sentido de organización y adaptación del razonamiento. Cuando más avanzamos en los estadios el ser humano va requiriendo cada vez más capacidades de razonamiento esto por el ambiente y la cultura que rodea al individuo de ahí la necesidad de la acomodación y la asimilación. La necesidad de estar en equilibro es fundamental para el avance del pensamiento, puesto que si nuestro esquema no da el resultado esperado el individuo se siente incómodo el mismo organiza, adapta, acomoda y asimila, esto hace que nuestro pensamiento se re-ajuste y avance. Esto es muy notorio a través de las experiencias personales y la madurez que se adquiere con las mismas. A todo el proceso anteriormente explicado se le conoce como funcionamiento intelectual. Estadios del desarrollo intelectual (Piaget). Estadio sensoriomotor (0-2 años): La inteligencia del niño es práctica, no comprende el hecho de que son los objetos ni que desaparezcan de su vista todos los problemas son resueltos a nivel acción. Estadio preoperatorio (2-7 años): Los niños ya comprenden la estadía de un objeto, además de que su comprensión es más compleja con lenguaje e imágenes mentales, aunque no es muy lógica. Estadio de las operaciones concretas (7-12 años): El pensamiento adquiere una secuencia lógica, pueden aplicar estos conocimientos o razonamiento lógico solo aquellos objetos con los cuales han tenido contacto con sus sentidos. Estadio de las operaciones formales (en la adolescencia): Los adolescentes adquieren una lógica formal y comienzan a tener una visión más abstracta del mundo que los rodea, además de tener la capacidad de manejar y verificar hipótesis.  Una característica muy importante de esta etapa es la capacidad de razonar en contra de los hechos.

Todos los individuos logran tener un desarrollo hasta cierto grado y de cierta manera de acuerdo con la sociedad que los rodea, en donde pueden influir las costumbres y las actividades sociales. Es muy importante reconocer que los conocimientos adquiridos por el niño son construidos con el apoyo de adultos más conocedores esto constituye el medio principal para el desarrollo intelectual. El ser humano tiene consigo desde el nacimiento funciones mentales inferiores las cuales se irán desarrollando de acuerdo con la interacción social, entre más conocimiento, mayor forma de tomar una acción y con ella más complejas funciones mentales. Sucesivamente la persona adquiere una habilidad mental la cual primeramente la manifestara con la sociedad (Inter psicológicamente) y después individualmente (intra psicológicamente). La sociedad empieza a tener mucho mayor importancia cuando nos referimos a las herramientas del pensamiento pues estas son adquiridas a través de la interacción, es decir, el lenguaje, las normas, los números, las palabras, los pensamientos lógicos son adquiridos a través de la socialización. Hay varias habilidades y herramientas que el niño adquiera a través del desarrollo proximal, es decir, aquellas actividades en donde el niño ocupa ayuda (son aquellas funciones las cuales no se han desarrollado completamente, pero se encuentran en el proceso de este). Las integraciones con los adultos y compañeros le ayudan al niño a alcanzar un nivel superior de funcionamiento. Para finalizar es muy importante cada cosa de lo anterior mencionado para poder lograr una conceptualización, en donde la parte de egocentrismo servida de gran importancia para la autorregulación del individuo. Todo esto se logrará con las herramientas y funciones adquiridas con la sociedad que nos rodea.

En el cuadro previo, se aprecia el enfoque que estos dos autores nos ofrecen respecto a la evolución del individuo, considerando tanto su dimensión social como biológica. A través de esta perspectiva, se puede comprender la diversidad de factores que inciden en la conducta y el pensamiento del adolescente que se encuentra en la escuela secundaria y son objeto de estudio de esta investigación.

CONCLUSIÓN.

Es crucial situar el aprendizaje en escenarios relevantes para los estudiantes. El uso de ejemplos vinculados con su entorno cotidiano no solo facilita la comprensión, sino que también despierta su interés y conecta los conceptos matemáticos con problemas reales. Este enfoque contextualizado fomenta la percepción de la matemática como una herramienta práctica y útil, capaz de resolver desafíos del mundo moderno. Las metodologías tradicionales deben complementarse con enfoques actuales, como la resolución de problemas, el aprendizaje basado en proyectos o el uso de tecnologías digitales. Estas herramientas promueven la participación de los estudiantes, fortalecen el pensamiento crítico y los preparan para enfrentar situaciones complejas de manera autónoma y creativa.

Cada estudiante aprende de manera diferente, por lo que es esencial que el docente ajuste sus estrategias didácticas a las necesidades y estilos de aprendizaje de su grupo. Evaluar y aprovechar las inteligencias múltiples, por ejemplo, permite personalizar la enseñanza y maximizar el potencial de cada alumno.

En conjunto, este enfoque integral garantiza que los estudiantes no solo adquieran conocimientos matemáticos, sino que también desarrollen competencias como la resolución de problemas, el pensamiento lógico y la autonomía, esenciales para su formación académica y personal.

REFERENCIAS.

Álvarez, J. R. (2020). Calcular la fiabilidad de un cuestionario o escala mediante SPSS: el coeficiente alfa de Cronbach. REIRE, 1-13. Obtenido de https://revistes.ub.edu/index.php/REIRE/article/view/reire2020.13.230048/31484

Anaya, A., & Huertas, C. (2010). ¿Motivar para aprobar o aprender? Estrategias de motivacion del aprendizaje para los estudiantes. Tecnologia. Ciencia Educativa., 5-14.

Arias-Gómez, J., Villasís-Keever, M. Á., & Miranda Novales, M. G. (2016). El protocolo de investigación III: la población de estudio. Alergia México, 1-7.

Azcona, M., & Manzini, F. y. (2013). PRECISIONES METODOLÓGICAS SOBRE LA UNIDAD DE ANÁLISIS Y LA UNIDAD DE OBSERVACIÓN. APLICACIÓN A LA INVESTIGACIÓN EN PSICOLOGIA, 1-10.

Azuero, Á. E. (2019). Significatividad del marco metodológico en el desarrollo de proyectos de investigación. Revista Arbitrada Interdisciplinaria KOINONIA, 1-18.

Bastar, S. G. (2012). Metodología de la investigación . México : Red tercer milenio.

Blácido, I. R. (2022). Métodos cientificos y su aplicación en la investigación pedagógica. Revista Dilemas Contemporáneos: Educación, Política y Valores, 1-19.

Castañeda, J. a. (2005). Reseña de "Como pensamos. Nueva expisición de la relacion entre pensamiento reflexivo y educación" de John Dewey. Revista interconinental de psicología y educación , 154-162.

Castro, E. P. (2006). Áprendizaje autorregulado: Una revisión Conceptual. Revista electrónica de psicologia Iztacala , 1-21.

Chaves, D. C. (2017). Delimitacion y justificación de problemas de intestigación en ciencias sociales. Ciencias Sociales, 3. Obtenido de https://www.redalyc.org/journal/153/15354681012/html/

Corrales, L. E. (2021). Evaluación formativa en la práctica pedagógica: una revisión bibliográfica. Revista pedagógica de la Universidad de Cienfuegos, 1-6.

Dewey, J. (1989). Cómo pensamos. Nueva exposicion de la relacion entre el pensamiento reflexivo y el proceso educativo. Barcelona, España: Paidós.

Freire, E. E. (2018). La hipotesis en la investigación. MENDIVE, 1-18.

Freire, E. E. (2022). El problema, el objetivo, la hipotesis las variables de la investigación. Guayaquil, Ecuador: EXCED.

García., J. E. (2020). Validez y confiabilidad en la recolección y análisis de datos bajo un enfoque cualitativo. Trascender, Contabilidad y Gestión, 1-19. Obtenido de https://www.scielo.org.mx/pdf/tcg/v5n15/2448-6388-tracender-15-79.pdf.

González, J. L. (2021). Diseño y metodología de investigación. Arequipa, Perú: ENFOQUES CONSULTING EIRL.

González, O. H. (2021). Aproximación a los distintos tipos de muestreo no probabilístico que existen . Revista Cubana de Medicina General Integral, 1-3.

Grajales, T. (23 de Diciembre de 2000). Tipos de investigación. Obtenido de Virtuarl Urbe: https://virtual.urbe.edu/tesispub/0103069/cap03.pdf

José Luis Arias González, M. R. (2022). Ciencia Latina Revista Científica Multidisciplinar, Ciudad de México, México. ISSN 2707-2207 / ISSN 2707-2215 (en línea), julio-Formulación de los objetivos específicos desde el alcance correlacional en trabajos de investigación. Ciencia Latina. Revista multidisciplinar., 1-11. Obtenido de http://revistasbolivianas.umsa.bo/scielo.php?script=sci_arttext&pid=S2304-37682011000700003&lng=en&nrm=iso&tlng=es.

Leandro, J. T. (14 de Enero de 2024). Fiabilidad de las escalas: interpretación y limitaciones del Alfa de Cronbach. Obtenido de researchgate.net: https://www.researchgate.net/profile/Jack-Torres-Leandro-2/publication/350590351_Fiabilidad_de_las_escalas_interpretacion_y_limitaciones_del_Alfa_de_Cronbach/links/60674db992851c91b19b8290/Fiabilidad-de-las-escalas-interpretacion-y-limitaciones-del-Alfa-d

Mercadé, A. (17 de Diciembre de 2019). Los 8 tipos de Inteligencia según Howard Gardner: la teoría de inteligencias multiples. Obtenido de UDGVIRTUAL: http://biblioteca.udgvirtual.udg.mx/jspui/handle/123456789/2943

Rodriguez, A. M. (2015). Diseño y validación de instrumentos de medicion . Revista Digital de Ciencia y Cultura de El Salvador, 1-22. Obtenido de http://redicces.org.sv/jspui/bitstream/10972/2105/1/2%20disenoyvalidacion_dialogos14.pdf

Romero, N. S. (2019). La Ética en la investigación cualitativa. Cuidarte, 1-9.

Sampieri, R. H. (2014). Métodologia de la investigación. En R. H. Sampieri, Métodologia de la investigación (págs. 170-191). Mexico : McGraw-Hill.

Sampieri, R. H. (2018). Metodología de la investigación las rutas cuantitativa, cualitativa y mixta. México : McGRAW-HILL INTERAMERICANA EDITORES, S.A. de C. V.

Sánchez, M. M. (2019). Estrategias de aprendizaje para el desarrollo de la autonomía de los estudiantes de secundaria. SciELO Analytics, 4-13.

SEP. (2022). Avance programa sintético de la fase 6. Ciudad de México: SEP.

Tejada, A. (2009). La planeación didáctica. En Cuadernos de formación de profesores , 1-10.

University, U. (15 de diciembre de 2023). Obtenido de https://gc.scalahed.com/recursos/files/r161r/w23608w/unidad2.pdf